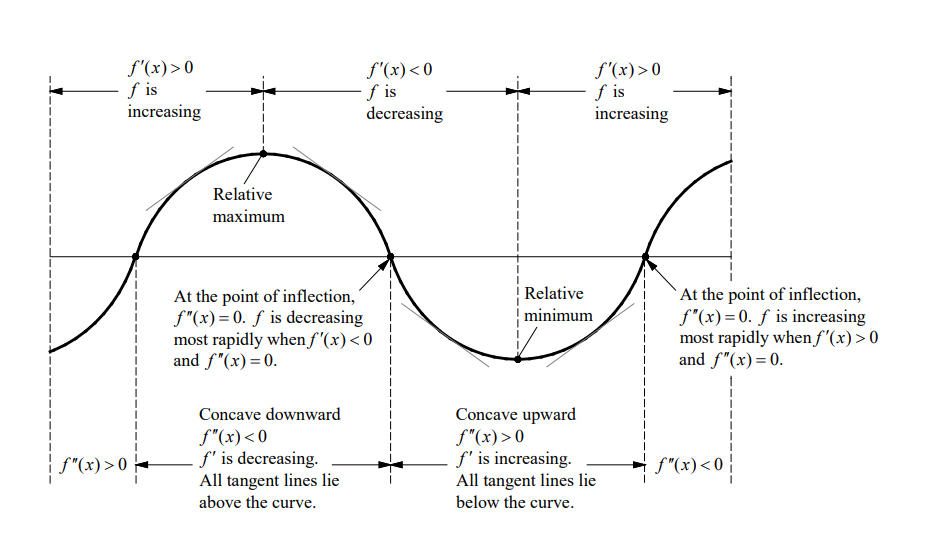
The Second Derivative Test
Test for Concavity
1. If $f^{\prime \prime}(x)>0$ for all $x$ in an open interval $I$, then the graph of $f$ is concave upward on $I$.
2. If $f^{\prime \prime}(x)<0$ for all $x$ in an open interval $I$, then the graph of $f$ is concave downward on $I$.
Definition of Points of Inflection
A point $P$ on a curve $y=f(x)$ is called a point of inflection if $f$ is continuous on $P$ and the curve changes from concave upward to concave downward or vice versa.
If $(c, f(c))$ is a point of inflection of the graph of $f$, then either $f^{\prime \prime}(x)=0$ or $f$ is not differentiable at $x=c$.
Second Derivative Test
Let $f$ be a function such that $f^{\prime}(c)=0$ and the second derivative of $f$ exists on an open interval containing $c$.
1. If $f^{\prime \prime}(c)>0$, then $f(c)$ is a relative minimum.
2. If $f^{\prime \prime}(c)<0$, then $f(c)$ is a relative maximum.
3. If $f^{\prime \prime}(c)=0$, the test fails. Use the First Derivative Test.
Example
- Let $f$ be the function given by $f(x)=3 x^5-5 x^3+3$.
(a) Find the relative maximum and minimum value of $f$.
(b) Find the intervals on which $f$ is increasing and decreasing.
(c) Find the $x$-coordinate of each inflection points on the graph of $f$.
(d) Find the intervals on which $f$ is concave upwards and concave downwards.
▶️Answer/Explanation
Solution
(a) Use the first derivative test to find the relative extreme values.
$
\begin{aligned}
& f^{\prime}(x)=15 x^4-15 x^2=15 x^2(x+1)(x-1) \\
& f^{\prime}(x)=0 \Rightarrow x=-1,0,1
\end{aligned}
$
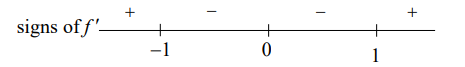
Since $f^{\prime}$ changes from positive to negative at $x=-1$, $f(-1)=5$ is a relative maximum.
The sign of $f^{\prime}$ does not change at $x=0$, so there is no maximum or minimum.
Since $f^{\prime}$ changes from negative to positive at $x=1$, $f(1)=1$ is a relative minimum.
(b) $f$ is increasing on $(\infty,-1)$ and $(1, \infty)$. $f$ is decreasing on $(-1,1)$.
(c) $f^{\prime \prime}(x)=60 x^3-30 x=30 x\left(2 x^2-1\right)$
$
f^{\prime \prime}(x)=0 \Rightarrow x=-\frac{\sqrt{2}}{2}, 0, \frac{\sqrt{2}}{2}
$
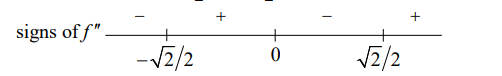
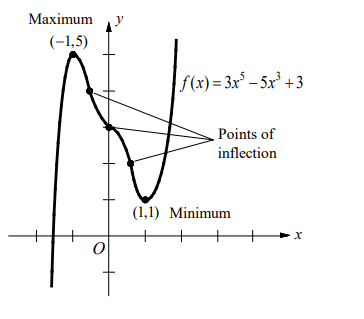
$f^{\prime \prime}$ changes from negative to positive at $x=-\sqrt{2} / 2$, from positive to negative at $x=0$, and from negative to positive at $x=\sqrt{2} / 2$, so, $-\sqrt{2} / 2,0$, and $\sqrt{2} / 2$ are the $x$-coordinate of the points of inflection.
(d) The graph of $f$ is concave downward on $(-\infty,-\sqrt{2} / 2)$ and $(0, \sqrt{2} / 2)$.
The graph of $f$ is concave upward on $(-\sqrt{2} / 2,0)$ and $(\sqrt{2} / 2, \infty)$.
Exercises – The Second Derivative Test
Multiple Choice Questions
- The graph of $y=x^4-2 x^3$ has a point of inflection at
(A) $(0,0)$ only
(B) $(0,0)$ and $(1,-1)$
(C) $(1,-1)$ only
(D) $(0,0)$ and $\left(\frac{3}{2},-\frac{27}{16}\right)$
▶️Answer/Explanation
Ans:B
Question
- If the graph of $y=a x^3-6 x^2+b x-4$ has a point of inflection at $(2,-2)$, what is the value of $a+b$ ?
(A) -2
(B) 3
(C) 6
(D) 10
▶️Answer/Explanation
Ans:D
Question
- At what value of $x$ does the graph of $f(x)=\sqrt{x}+\frac{1}{\sqrt{x}}$ have a point of inflection?
(A) $\frac{1}{2}$
(B) 1
(C) 3
(D) $\frac{7}{2}$
▶️Answer/Explanation
Ans:C
Question
- The graph of $y=3 x^5-40 x^3-21 x$ is concave up for
(A) $x<0$
(B) $x>2$
(C) $x<0$ or $0<x<2$
(D) $-2<x<0$ or $x>2$
▶️Answer/Explanation
Ans:D
Question
- Let $f$ be a twice differentiable function such that $f(1)=7$ and $f(3)=12$. If $f^{\prime}(x)>0$ and $f^{\prime \prime}(x)<0$ for all real numbers $x$, which of the following is a possible value for $f(5)$ ?
(A) 16
(B) 17
(C) 18
(D) 19
▶️Answer/Explanation
Ans:B
