7.1 Slope Field
A first order differential equation of the form $y^{\prime}=f(x, y)$ says that the slope of a solution curve at a point $(x, y)$ on the curve is $f(x, y)$. If we draw short line segments with slope $f(x, y)$ at several points $(x, y)$, the result is called a slope field.
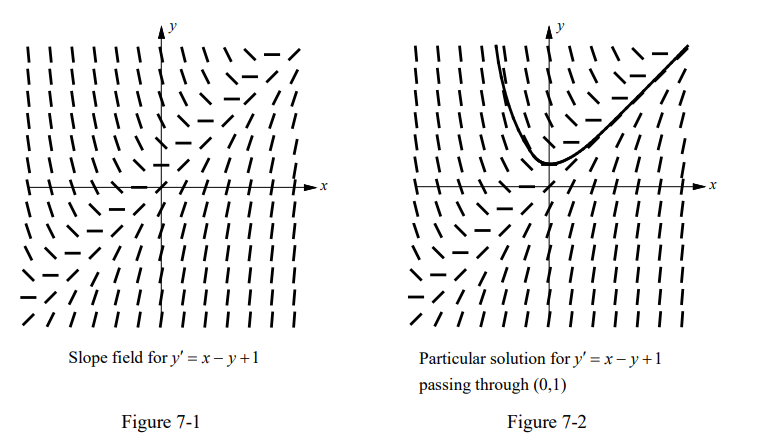
Figure 7-1 shows a slope field for the differential equation $y^{\prime}=x-y+1$ Figure
7-2 shows a particular solution curve through the point $(0,1)$.
Example1
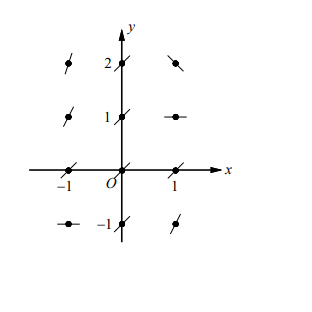
- On the axes provided, sketch a slope field for the differential equation $y^{\prime}=1-x y$.
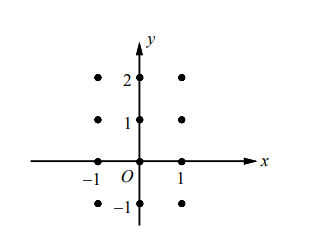
▶️Answer/Explanation
Solution
Make a table showing the slope at the points shown on the graph.
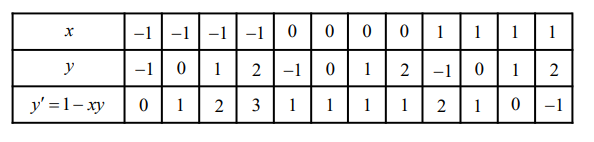
Draw the line segments at the points with their respective slopes.
Example 2
- On the axes provided, sketch a slope field for the differential equation $y^{\prime}=y+x y$.
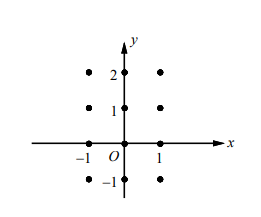
▶️Answer/Explanation
Solution
Make a table showing the slope at the points shown on the graph.
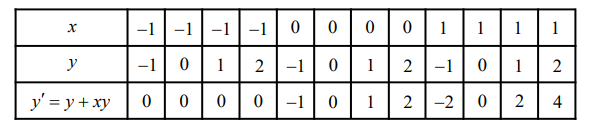
Draw the line segments at the points with their respective slopes.
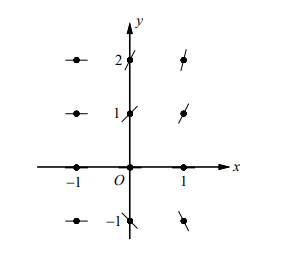
Example 3
- Multiple Choice Questions
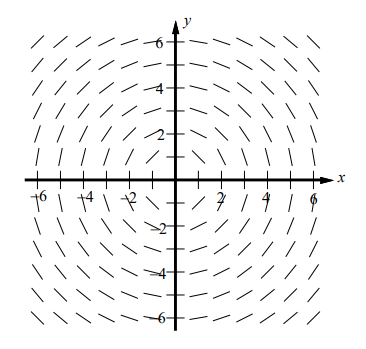
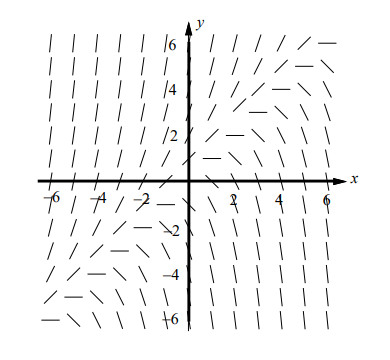
1. Shown above is a slope field for which of the following differential equations?
(A) $\frac{d y}{d x}=\frac{x}{y}$ (B) $\frac{d y}{d x}=-\frac{x}{y}$ (C) $\frac{d y}{d x}=\frac{x^2}{y}$ (D) $\frac{d y}{d x}=-\frac{x^2}{y}$
▶️Answer/Explanation
Ans:D
Example 4
2. Shown above is a slope field for which of the following differential equations?
(A) $\frac{d y}{d x}=x+y$
(B) $\frac{d y}{d x}=x-y$
(C) $\frac{d y}{d x}=-x+y$
(D) $\frac{d y}{d x}=x^2-y$
▶️Answer/Explanation
Ans:B
Example 5
- 3. On the axis provided, sketch a slope field for the differential equation $\frac{d y}{d x}=y-x^2$.
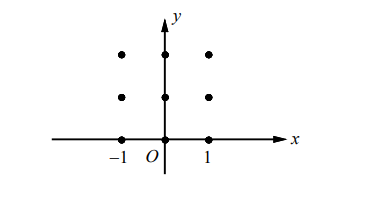
▶️Answer/Explanation
Ans:C
Example 6
- On the axis provided, sketch a slope field for the differential equation $\frac{d y}{d x}=x^2+y^2$.
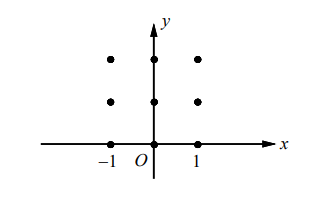
▶️Answer/Explanation
Ans:A