Limit Laws
Let c and k be real numbers and the limits \(\underset{x\rightarrow c}{lim}f\left ( x \right )\) and \(\underset{x\rightarrow c}{lim}g\left ( x \right )\) exist.
Then
- \(\underset{x\rightarrow c}{lim}\left [ f\left ( x \right )\pm g\left ( x \right )\right ]=\underset{x\rightarrow c}{lim}f\left ( x \right )\pm \underset{x\rightarrow c}{lim}g\left ( x \right )\)
- \(\underset{x\rightarrow c}{lim}\left [ f\left ( x \right )\cdot g\left ( x \right )\right ]=\underset{x\rightarrow c}{lim}f\left ( x \right )\cdot \underset{x\rightarrow c}{lim}g\left ( x \right )\)
- \(\underset{x\rightarrow c}{lim}\left [ kf\left ( x \right ) \right ]=k\underset{x\rightarrow c}{lim}f\left ( x \right )\)
- \(\underset{x\rightarrow c}{lim}\frac{f\left ( x \right )}{g\left ( x \right )}=\frac{\underset{x\rightarrow c}{lim}f\left ( x \right )}{\underset{x\rightarrow c}{lim}g\left ( x \right )}\)
- \(\underset{x\rightarrow c}{lim}\left [ f\left ( x \right ) \right ]^{^{n}}=\left [ \underset{x\rightarrow c}{lim}f\left ( x \right ) \right ]^{n}\)
- \(\underset{x\rightarrow c}{lim}\sqrt[n]{f\left ( x \right )}=\sqrt[n]{\underset{x\rightarrow c}{lim}{f\left ( x \right )}}\)
Special Trigonometric Limits
- \(\underset{x\rightarrow 0}{lim}\frac{sin x}{x}=1\)
- \(\underset{x\rightarrow 0}{lim}\frac{1-cos x}{x}=0\)
Example 1
- Find the limits.
(a) \(\underset{x\rightarrow 2}{lim}\frac{x^{2}+3x-10}{x-2}\)
(b) \(\underset{x\rightarrow 1}{lim}\frac{\sqrt{x+3-2}}{x-1}\)
▶️Answer/Explanation
Solution

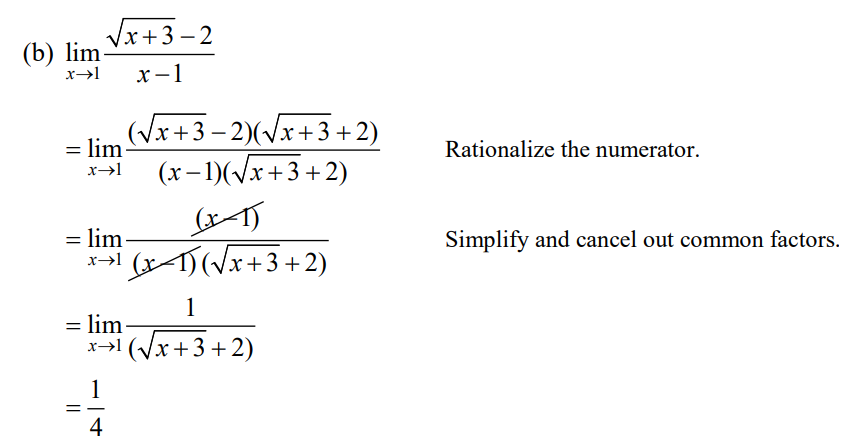
Example 2
- Find the limits.
(a) \(\underset{x\rightarrow 0}{lim}\frac{sin 4x}{3x}\)
(b) \(\underset{x\rightarrow 0}{lim}\frac{tan x}{x}\)
(c) \(\underset{x\rightarrow \pi /4}{lim}\frac{tan x-1}{sinx-cosx}\)
▶️Answer/Explanation
Solution

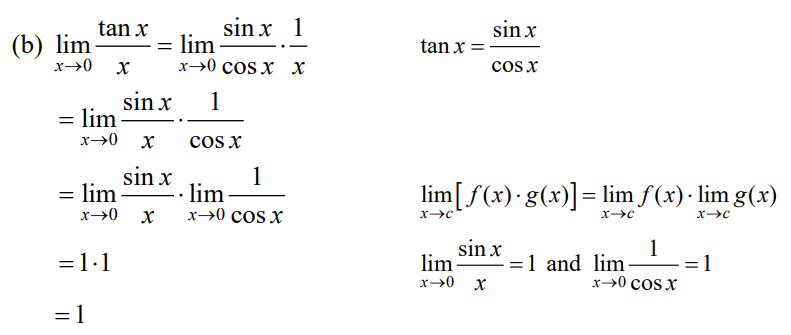
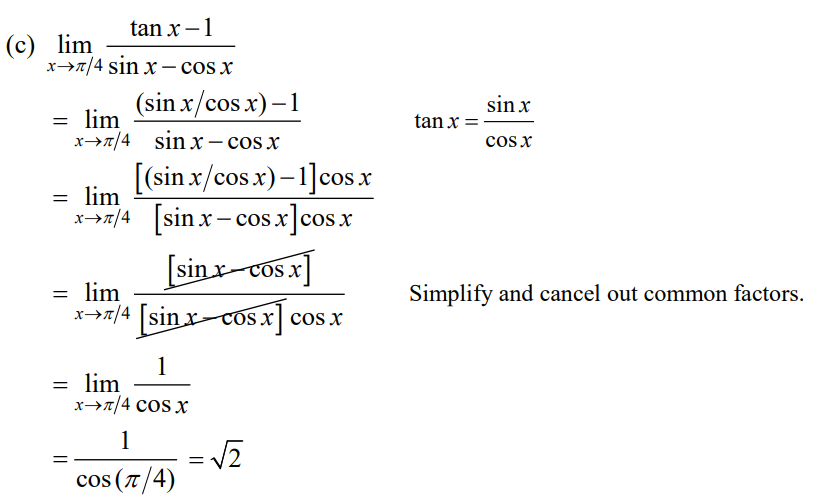
Exercises – Calculating Limits Using the Limit Laws
Multiple Choice Questions
Question
- \(\underset{x\rightarrow \pi /3}{lim}\frac{sin\left ( \frac{\pi }{3} -x\right )}{( \frac{\pi }{3} -x)}=\)
(A) −1 (B) 0 (C) \(\frac{\sqrt{3}}{2}\) (D) 1
▶️Answer/Explanation
Ans:
1. D
Question
- \(\underset{x\rightarrow 0}{lim}\frac{sin3x}{sin2x}=\)
(A) \(\frac{2}{3}\) (B) 1 (C) \(\frac{3}{2}\) (D) nonexistent
▶️Answer/Explanation
Ans:
2. C
Question
- \(\underset{x\rightarrow 0}{lim}\frac{\sqrt{4+x-2}}{x}=\)
(A) \(\frac{1}{8}\) (B) \(\frac{1}{4}\) (C) \(\frac{1}{2}\) (D) nonexistent
▶️Answer/Explanation
Ans:
3. B
Question
- \(\underset{x\rightarrow 1}{lim}\frac{\sqrt{3+x-2}}{x^{3}-1}=\)
(A) \(\frac{1}{12}\) (B) \(\frac{1}{6}\) (C) \(\sqrt{3}\) (D) nonexistent
▶️Answer/Explanation
Ans:
4. A
Question
- \(\underset{θ\rightarrow 0}{lim}\frac{θ+θ cosθ}{sin θ cos θ}=\)
(A) \(\frac{1}{4}\) (B) \(\frac{1}{2}\) (C) 1 (D) 2
▶️Answer/Explanation
Ans:
5. D
Question
- \(\underset{x\rightarrow 0}{lim}\frac{tan 3x}{x}=\)
(A) 0 (B) \(\frac{1}{3}\) (C) 1 (D) 3
▶️Answer/Explanation
Ans:
6. D
Question
- \(\underset{x\rightarrow 3}{lim}\frac{\frac{1}{x}-\frac{1}{3}}{x-3}=\)
(A) \(-\frac{1}{9}\) (B) \(\frac{1}{9}\) (C) -9 (D) 9
▶️Answer/Explanation
Ans:
7. A
Free Response Questions
Question
- If \(\underset{x\rightarrow 0}{lim}\frac{\sqrt{2+ax-\sqrt{2}}}{x}=\sqrt{2}\) what is the value of a ?
▶️Answer/Explanation
Ans:
8. 4
Question
- Find \(\underset{h\rightarrow 0}{lim}\frac{f\left ( x+h \right )-f\left ( x \right )}{h},\) if \(f\left ( x \right )=\sqrt{2x+1}\).
▶️Answer/Explanation
Ans:
9. \(\frac{1}{\sqrt{2x+1}}\)
Question
- Find \(\underset{x\rightarrow 0}{lim}\frac{f\left ( x \right )-g\left ( x \right )}{\sqrt{g\left ( x \right )+7}}\), if \(\underset{x\rightarrow 0}{lim}f\left ( x \right )=2\) and \(\underset{x\rightarrow 0}{lim}g\left ( x \right )=-3\).
▶️Answer/Explanation
Ans:
10. 5/2
Question
- Find \(\underset{x\rightarrow \sqrt{3}}{lim}g\left ( x \right )\), if \(\underset{x\rightarrow \sqrt{3}}{lim} \frac{1}{x^{2}+g\left ( x \right )}=\frac{1}{5}\).
▶️Answer/Explanation
Ans:
11. 2
