Properties of Definite Integral
Definition
$
\int_a^a f(x) d x=0 \quad \int_a^b f(x) d x=-\int_b^a f(x) d x
$
Constant Multiple
$
\int_a^b c d x=c(b-a) \quad \int_a^b c f(x) d x=c \int_a^b f(x) d x
$
Sum and Difference
$
\int_a^b[f(x) \pm g(x)] d x=\int_a^b f(x) d x \pm \int_a^b g(x) d x
$
Additivity
$
\int_a^b f(x) d x+\int_b^c f(x) d x=\int_a^c f(x) d x
$
Integrals of Symmetric Functions
If $f$ is even $f(-x)=f(x)$, then $\int_{-a}^a f(x) d x=2 \int_0^a f(x) d x$
If $f$ is odd $f(-x)=-f(x)$, then $\int_{-a}^a f(x) d x=0$
Comparison Property
If $f(x) \geq 0$ for $a \leq x \leq b$, then $\int_a^b f(x) d x \geq 0$
If $f(x) \geq g(x)$ for $a \leq x \leq b$, then $\int_a^b f(x) d x \geq \int_a^b g(x) d x$
If $m \leq f(x) \leq M$ for $a \leq x \leq b$, then $m(b-a) \leq \int_a^b f(x) d x \leq M(b-a)$
Example1
- Suppose that $\int_{-3}^4 f(x) d x=5, \int_{-3}^4 g(x) d x=-4$, and $\int_{-3}^1 f(x) d x=2$.
Find (a) $\int_{-3}^4[2 f(x)-3 g(x)] d x$
(b) $\int_1^4 f(x) d x$
(c) $\int_{-3}^4[g(x)+2] d x$.
▶️Answer/Explanation
Solution
$
\begin{aligned}
& \int_{-3}^4[2 f(x)-3 g(x)] d x=\int_{-3}^4 2 f(x) d x-\int_{-3}^4 3 g(x) d x \\
& =2 \int_{-3}^4 f(x) d x-3 \int_{-3}^4 g(x) d x=2 \cdot 5-3 \cdot(-4)=22
\end{aligned}
$
(a)
$
\begin{aligned}
(b) & \int_{-3}^4 f(x) d x=\int_{-3}^1 f(x) d x+\int_1^4 f(x) d x \\
& \Rightarrow 5=2+\int_1^4 f(x) d x \Rightarrow \int_1^4 f(x) d x=3
\end{aligned}
$
(c) $\int_{-3}^4[g(x)+2] d x=\int_{-3}^4 g(x) d x+\int_{-3}^4 2 d x=-4+2(4+3)=10$
Example2
- If $\int_a^b f(x) d x=2 a-5 b$, then $\int_a^b[f(x)-2] d x=$
(A) $-7 b$
(B) $-3 b$
(C) $4 a-7 b$
(D) $4 a-3 b$
▶️Answer/Explanation
Ans:C
Example3
- If $\int_1^6 f(x) d x=\frac{15}{2}$ and $\int_6^4 f(x) d x=5$, then $\int_1^4 f(x) d x=$
(A) $\frac{5}{2}$
(B) $\frac{9}{2}$
(C) $\frac{19}{2}$
(D) $\frac{25}{2}$
Ans:D
Example4
- If $\int_{-2}^6 f(x) d x=10$ and $\int_2^6 f(x) d x=3$, then $\int_2^6 f(4-x) d x=$
(A) 3
(B) 6
(C) 7
(D) 10
▶️Answer/Explanation
Ans:C
Example5
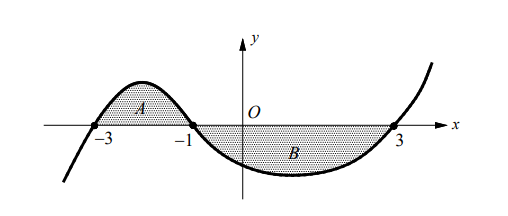
The graph of $y=f(x)$ is shown in the figure above. If $A$ and $B$ are positive numbers that represent the areas of the shaded regions, what is the value of $\int_{-3}^3 f(x) d x-2 \int_{-1}^3 f(x) d x$, in terms of $A$ and $B$ ?
(A) $-A-B$
(B) $A+B$
(C) $A-2 B$
(D) $A-B$
▶️Answer/Explanation
Ans:B
