Derivatives of Trigonometric Functions
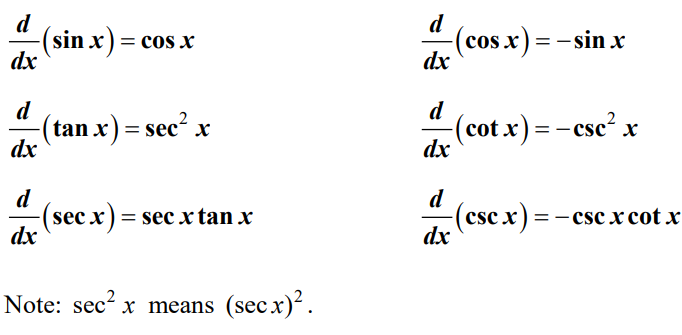
Example 1
- Find \(\frac{dy}{dx}\) for \(y=x^{2}sinx+2xcosx.\)
▶️Answer/Explanation
Solution
\(\frac{dy}{dx}=x^{2}cos x + sin x\cdot 2x+2\left ( x\left ( -sinx \right ) +cosx\cdot 1\right )\)
\(=x^{2}cos x + 2xsinx-2xsinx+2cosx\)
\(=x^{2}cos x + 2cosx\)
Example 2
- Find \({y}’\) if \(y=tan^{2}\left ( x^{3} \right ).\)
▶️Answer/Explanation
Solution
\(y=tan^{2}\left ( x^{3} \right )=\left [ tan\left ( x^{3} \right ) \right ]^{2}\) \(tan^{2}x=\left ( tanx \right )^{2}\)
\({y}’=2\left [ tan\left ( x^{3} \right ) \right ]\frac{d}{dx}\left ( tan\left ( x^{3} \right ) \right )\) Power Chain Rule
\(=2tan\left ( x^{3} \right )sec^{2}\left ( x^{3} \right )\frac{d}{dx}\left ( x ^{3}\right )\) Chain Rule
\(=2tan\left ( x^{3} \right )sec^{2}\left ( x^{3} \right )\left ( 3x^{2} \right )\) Power Rule
\(=6x^{2}tan\left ( x^{3} \right )sec^{2}\left ( x^{3} \right )\)
Exercises – Derivatives of Trigonometric Functions
Multiple Choice Questions
1. \(\underset{h\rightarrow 0}{lim}\frac{cos\left ( \frac{\pi }{3}+h \right )-\frac{1}{2}}{h}=\)
(A) \(-\frac{1}{2}\) (B) \(-\frac{\sqrt{3}}{2}\) (C) \(\frac{1}{2}\) (D) \(\frac{\sqrt{3}}{2}\)
▶️Answer/Explanation
Ans:
1. B
2. \(\underset{h\rightarrow 0}{lim}\frac{sin2\left ( x+h \right )-sin2x}{h}=\)
(A) 2sin 2x (B) −2sin 2x (C) 2cos 2x (D) −2cos 2x
▶️Answer/Explanation
Ans:
2. C
3. If \(f\left ( x \right )=sin\left ( cos2x \right )\), then \({f}’\left ( \frac{\pi }{4} \right )=\)
(A) 0 (B) −1 (C) 1 (D) −2
▶️Answer/Explanation
Ans:
3. D
4. If y=a sin x + b cos x, then y + y ” =
(A) 0 (B) 2 sin a x (C) 2 cos b x (D) −2 sin a x
▶️Answer/Explanation
Ans:
4. A
5. \(\frac{d}{dx}sec^{2}\left ( \sqrt{x} \right )=\)
(A) \(\frac{2sec\left ( \sqrt{x} \right )tan\left ( \sqrt{x} \right )}{\sqrt{x}}\)
(B) \(\frac{2sec^{2}\left ( \sqrt{x} \right )tan\left ( \sqrt{x} \right )}{\sqrt{x}}\)
(C) \(\frac{sec^{2}\left ( \sqrt{x} \right )tan\left ( \sqrt{x} \right )}{\sqrt{x}}\)
(D) \(\frac{sec\left ( \sqrt{x} \right )tan\left ( \sqrt{x} \right )}{\sqrt{x}}\)
▶️Answer/Explanation
Ans:
5. C
6. \(\frac{d}{dx}\left [ x^{2}cos2x \right ]=\)
(A) −2x sin 2x
(B) 2x (-x sin 2x + cos 2x)
(C) 2x (x sin 2x – cos 2x)
(D) 2x (x sin 2x – cos 2x)
▶️Answer/Explanation
Ans:
6. B
7. If \(f\left (\Theta \right )=cos\pi -\frac{1}{2cos\Theta }+\frac{1}{3tan\Theta }\), then \({f}’\left ( \frac{\pi }{6} \right )=\)
(A) \(\frac{1}{2}\) (B) 1 (C) \(\frac{4}{\sqrt{3}}\) (D) \(2\sqrt{3}\)
▶️Answer/Explanation
Ans:
7. B
Free Response Questions
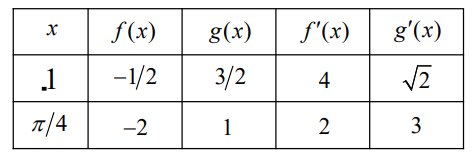
8. The table above gives values of f , f ′ , g , and g′ at selected values of x .
Find \({h}’\left ( \frac{\pi }{4} \right )\), if \(h\left ( x \right )=f\left ( x \right )\cdot g\left ( tanx \right ).\)
▶️Answer/Explanation
Ans:
8. \(-4\sqrt{4}+3\)
9. Find the value of the constants a and b for which the function
\(f\left ( x \right )=\left\{\begin{matrix}sin x, & x< \pi \\ax + b, & x\geq \pi\end{matrix}\right.\) is differentiable at \(x=\pi .\)
▶️Answer/Explanation
Ans:
9. a = −1
9. b = \(\pi\)
