Definite Integral, Area Under a Curve, and Application
Definition of a Definite Integral
If $f$ is a continuous function defined for $a \leq x \leq b$, then the definite integral of $f$ from $a$ to $b$ is
$
\int_a^b f(x) d x=\lim _{n \rightarrow \infty} \sum_{i=1}^n f\left(c_i\right) \Delta x,
$
where $c_i=a+i \Delta x$ and $\Delta x=(b-a) / n$.
If $y=f(x)$ is continuous and nonnegative over a closed interval $[a, b]$ then the area of the region bounded by the graph of $f$, the $x$-axis, and the vertical lines $x=a$ and $x=b$ is given by
$
\text { Area }=\int_a^b f(x) d x
$
If $f(x)$ takes on both positive and negative values over a closed interval $[a, b]$, then the area of the region bounded by the graph of $f$ and the $x$-axis is obtained by adding the absolute value of the definite integral over each subinterval where $f(x)$ does not change sign.
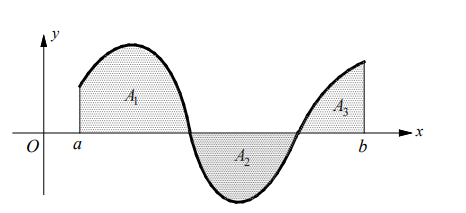
The figure above shows how both the total area and the value of definite integral can be interpreted in terms of areas between the graph of $f(x)$ and the $x$-axis.
The definite integral of $f(x)$ over $[a, b]=\int_a^b f(x) d x=A_1-A_2+A_3$.
The total area between the curve and the $x$-axis over $[a, b]=\int_a^b|f(x)| d x=A_1+A_2+A_3$.
Application of Definite Integral
If the population density of a region at a distance $x$ from a straight road is $D(x)$, then the total population of the region between $x=a$ and $x=b$ is given by
Total Population $=\int_a^b f(x) \cdot D(x) d x$
If the population density of a circular region at a distance $r$ from the center is $D(r)$, then the total population of the circular region between $r=a$ and $r=b$ is given by
Total Population $=2 \pi \int_a^b r D(r) d r$
Example1
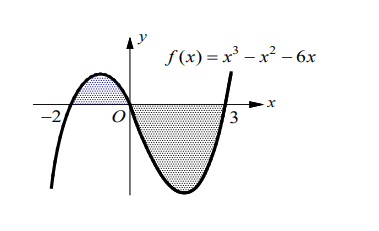
- The figure on the right shows the graph of $f(x)=x^3-x^2-6 x$
(a) Find the definite integral of $f(x)$ on $[-2,3]$.
(b) Find the area between the graph of $f(x)$ and the $x$-axis on $[-2,3]$.
▶️Answer/Explanation
Solution
$
\text { (a) } \begin{aligned}
\int_{-2}^3\left(x^3-x^2-6 x\right) d x=\left[\frac{x^4}{4}-\frac{x^3}{3}-3 x^2\right]_{-2}^3 \\
=\left(\frac{81}{4}-\frac{27}{3}-27\right)-\left(\frac{16}{4}+\frac{8}{3}-12\right)=-\frac{125}{12}
\end{aligned}
$
$
\begin{aligned}
(b) & \text { Area }=\int_{-2}^3\left|x^3-x^2-6 x\right| d x=\left|\left[\frac{x^4}{4}-\frac{x^3}{3}-3 x^2\right]_{-2}^0\right|+\left|\left[\frac{x^4}{4}-\frac{x^3}{3}-3 x^2\right]_0^3\right| \\
& =\left|\frac{16}{3}\right|+\left|-\frac{63}{4}\right|=\frac{253}{12}
\end{aligned}
$
Example2
A rectangular region located beside a highway and between two straight roads 11 miles apart are shown in the figure above. The population density of the region at a distance $x$ miles from the highway is given by $D(x)=15 x \sqrt{x}-3 x^2$, where $0 \leq x \leq 25$. How many people live between 16 to 25 miles from the highway?
▶️Answer/Explanation
Population $=\int_a^b f(x) \cdot D(x) d x$
$=\int_{16}^{25} 11\left(15 x \sqrt{x}-3 x^2\right) d x \quad f(x)=11$ and $D(x)=15 x \sqrt{x}-3 x^2$
$\begin{aligned} & =\int_{16}^{25} 11\left(15 x^{3 / 2}-3 x^2\right) d x \\ & =11\left[15\left(\frac{2}{5}\right) x^{5 / 2}-x^3\right]_{16}^{25}=11\left[6 x^{5 / 2}-x^3\right]_{16}^{25} \\ & =11\left[\left\{6(25)^{5 / 2}-(25)^3\right\}-\left\{6(16)^{5 / 2}-(16)^3\right\}\right] \\ & =11[3,125-2,048] \\ & =11,847\end{aligned}$
Example3
- $
\int_0^3 \frac{d x}{\sqrt{1+x}}=
$
(A) 2
(B) 2.5
(C) 3
(D) 4
▶️Answer/Explanation
Ans:A
Example4
- The area of the region in the first quadrant enclosed by the graph of $f(x)=4 x-x^3$ and the $x$-axis is
(A) $\frac{11}{4}$
(B) $\frac{7}{2}$
(C) 4
(D) $\frac{11}{2}$
▶️Answer/Explanation
Ans:C
Example5
- $
\int_0^5 \sqrt{25-x^2} d x=
$
(A) $\frac{25 \pi}{8}$
(B) $\frac{25 \pi}{4}$
(C) $\frac{25 \pi}{2}$
(D) $25 \pi$
▶️Answer/Explanation
Ans:B
Example6
- The population density of a circular region is given by $f(r)=10-3 \sqrt{r}$ people per square mile, where $r$ is the distance from the center of the city, in miles. Which of the following expressions gives the number of people who live within a 3 mile radius from the center of the city?
(A) $\pi \int_0^3 r^2(10-3 \sqrt{r}) d r$
(B) $\pi \int_0^3(r+3)^2(10-3 \sqrt{r}) d r$
(C) $2 \pi \int_0^3(r+3)(10-3 \sqrt{r}) d r$
(D) $2 \pi \int_0^3 r(10-3 \sqrt{r}) d r$
▶️Answer/Explanation
Ans:D

