Definition of Continuity
A function f is continuous at c if the following three conditions are met.
- f (c) is defined
- \(\underset{x\rightarrow c}{lim} f\left ( x \right )\) exists
- \(\underset{x\rightarrow c}{lim} f\left ( x \right )=f\left ( c \right )\)
Intermediate Value Theorem
If f is continuous on the closed interval [a,b] and k is any number between f (a) and f (b), then there is at least one number c in [a,b] such that f (c) = k.
Specifically, if f is continuous on [a,b] and f (a) and f (b) differ in sign, the Intermediate Value Theorem guarantees the existence of at least one zero of f in the closed interval [a,b].
Example 1
- For what values of a is \(f\left ( x \right )=\left\{\begin{matrix}x^{2}, & x\leq 1\\ax+2, & 1< x\leq 3\end{matrix}\right.\) continuous at x = 1 ?
▶️Answer/Explanation
Solution
For f to be continuous at x = 1, \(\underset{x\rightarrow 1}{lim}f\left ( x \right )\) must equal f (1).
1. \(f\left ( 1 \right )=\left ( 1 \right )^{2}=1\)
2. \(\underset{x\rightarrow 1}{lim}f\left ( x \right )\) exists if \(\underset{x\rightarrow 1^{-}}{lim}f\left ( x \right )=\underset{x\rightarrow 1^{+}}{lim}f\left ( x \right ).\)
\(\underset{x\rightarrow 1^{-}}{lim}f\left ( x \right )=\underset{x\rightarrow 1^{-}}{lim}x^{2}=1\)
\(\underset{x\rightarrow 1^{+}}{lim}f\left ( x \right )=\underset{x\rightarrow 1^{+}}{lim}\left ( ax+2 \right )=a+2\)
\(\underset{x\rightarrow 1^{-}}{lim}f\left ( x \right )=\underset{x\rightarrow 1^{+}}{lim}f\left ( x\right )\Rightarrow 1=a+2\Rightarrow a=-1\)
3. \(\underset{x\rightarrow 1}{lim}f\left ( x \right )=1=f\left ( 1 \right )\)
Therefore f (x) is continuous at x = 1 if a = -1.
Example 2
- Let f be a function given by \(f\left ( x \right )=x^{3}-4x+2\). Use the Intermediate Value Theorem to show that there is a root of the equation on [0,1] .
▶️Answer/Explanation
Solution
f (x) is continuous on [0,1] and \(f\left ( 0\right )=2> 0\) and \(f\left ( 1\right )=-1< 0\).
By the Intermediate Value Theorem, \(f\left ( x \right )=0\) for at least one value c between 0 and 1. \(f\left ( 1 \right )=-1< f\left ( c \right )=0< f\left ( 0 \right )=2\)
Using a graphing calculator, we find that \(c\approx 0.539\), which is between 0 and 1.
Exercises – Properties of Continuity and Intermediate Value Theorem
Multiple Choice Questions
Question
- Let f be a function defined by \(f\left ( x \right )=\left\{\begin{matrix}\frac{x^{2}-a^{2}}{x-a}, & if x\neq a\\4 & if x = a\end{matrix}\right.\). If f is continuous for all real numbers x , what is the value of a ?
(A) \(\frac{1}{2}\) (B) 0 (C) 1 (D) 2
▶️Answer/Explanation
Ans:
1. D
Question
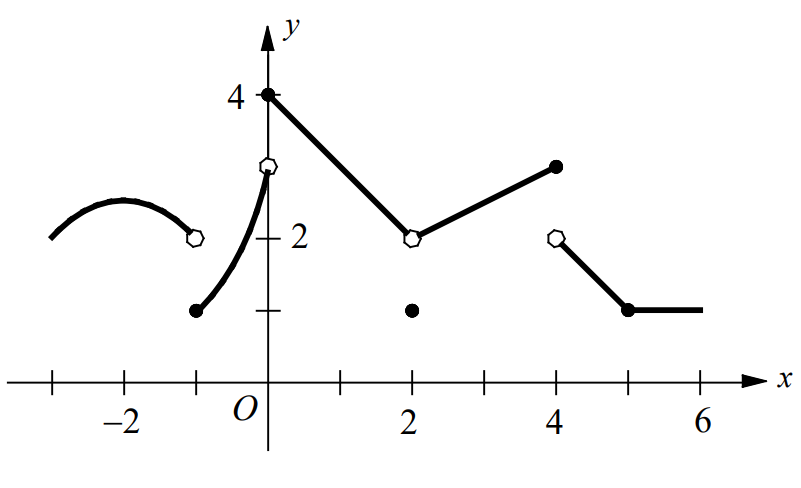
- The graph of a function f is shown above. If \(\underset{x\rightarrow a}{lim}f\left ( x \right )\) exists and f is not continuous at x = a, then a =
(A) -1 (B) 0 (C) 2 (D) 4
▶️Answer/Explanation
Ans:
2. C
Question
- If \(f\left ( x \right )=\left\{\begin{matrix}\frac{\sqrt{3x-1}-\sqrt{2x}}{x-1}, & for x\neq 1\\a, & for x = 1\end{matrix}\right.,\) and if f is continuous at x = 1 , then a =
(A) \(\frac{1}{4}\) (B) \(\frac{\sqrt{2}}{4}\) (C) \(\sqrt{2}\) (D) 2
▶️Answer/Explanation
Ans:
3. B
Question
- Let f be a continuous function on the closed interval [−2,7]. If f (-2) = 5 and f (7) = -3, then the Intermediate Value Theorem guarantees that
(A) f′(c) = 0 for at least one c between −2 and 7
(B) f′(c) = 0 for at least one c between −3 and 5
(C) f′(c) = 0 for at least one c between −3 and 5
(D) f′(c) = 0 for at least one c between −2 and 7
▶️Answer/Explanation
Ans:
4. D
Free Response Questions
Question
- Let g be a function defined by \(g\left ( x \right )=\left\{\begin{matrix}\frac{\pi sin x}{x}, & if x< 0\\a-bx, & if 0\leq x< 1.\\arctan x, & if x\geq 1\end{matrix}\right.\)
If g is continuous for all real numbers x , what are the values of a and b ?
▶️Answer/Explanation
Ans:
5. \(a=\pi , b=\frac{3\pi }{4}\)
Question
- Evaluate \(\underset{a\rightarrow 0}{lim}\frac{-1+\sqrt{1+a}}{a}\).
▶️Answer/Explanation
Ans:
6. \(\frac{1}{2}\)
Question
- What is the value of a , if \(\underset{x\rightarrow 0}{lim}\frac{\sqrt{ax+9-3}}{x}=1\)?
▶️Answer/Explanation
Ans:
7. 6
