Definition of Average Rate of Change
The expression \(\frac{f\left ( a+h \right )-f\left ( a \right )}{h}\) is called the difference quotient for f at a and represents the average rate of change of y = f (x) from a to a + h.
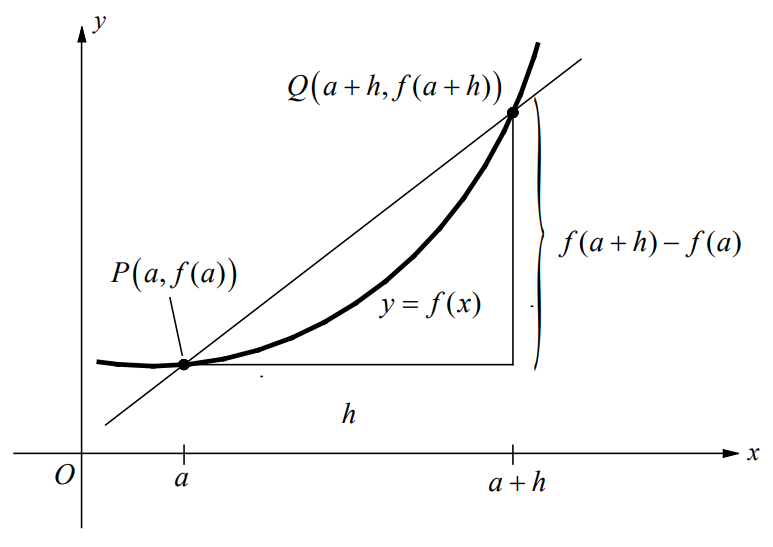
Geometrically, the rate of change of f from a to a + h is the slope of the secant line through the points \(P\left ( a,f\left ( a \right ) \right )\) and \(Q\left ( a+h,f\left ( a+h \right ) \right )\).
If f (t) is the position function of a particle that is moving on a straight line, then in the time interval from t = a to t = a + h, the change in position is f (a+h) – f (a), and the average velocity of the particle over the time interval is
average velocity = \(\frac{displacement}{time}=\frac{f\left ( a+h \right )-f\left ( a \right )}{h}\).
- Example 1
The displacement of a particle moving in a straight line is given by the equation of motion \(f\left ( t \right )=t^{3}-4t+3\). Find the average velocity of the particle over the interval \(0\leq t\leq 4\).
▶️Answer/Explanation
Solution
Average velocity = \(\frac{f\left ( 4 \right )-f\left ( 0 \right )}{4-0}=\frac{\left ( 64-16+3 \right )-3}{4-0}\)
= 12
Exercises – Rate of Change
Multiple Choice Questions
- Question
1. The traffic flow at a particular intersection is modeled by the function f defined by f (t) = \(25+6cos(\frac{x}{3})\) for \(0\leq t\leq 120\). What is the average rate of change of the traffic flow over the time interval \(30\leq t\leq 40\).
(A) 0.743 (B) 0.851 (C) 0.935 (D) 1.176
▶️Answer/Explanation
Ans:
1. C
Question
- 2. The rate of change of the altitude of a hot air balloon rising from the ground is given by \(y(t)=t^{3}-3t^{2}+3t\) for \(0\leq t\leq 10\). What is the average rate of change in altitude of the balloon over the time interval \(0\leq t\leq 10\).
(A) 56 (B) 73 (C) 85 (D) 94
▶️Answer/Explanation
Ans:
2. B
Question
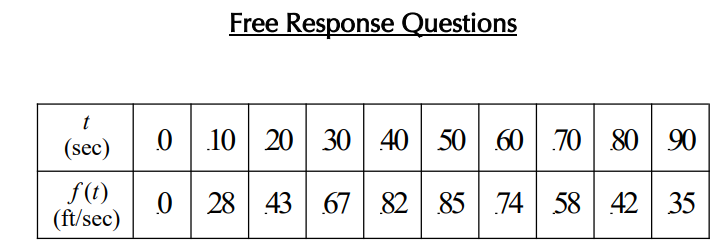
3.
- The table above shows the velocity of a car moving on a straight road. The car’s velocity v is measured in feet per second.
(a) Find the average velocity of the car from t = 60 to t = 90.
(b) The instantaneous rate of change of f (See Ch. 2.1 for an explanation of instantaneous rate of change) with respect to x at x = a can be approximated by finding the average rate of change of f near x = a. Approximate the instantaneous rate of change of f at x = 40 using two points, x = 30 and x = 50.
▶️Answer/Explanation
Ans:
3. (a) −1.3 ft /sec
3. (b) 0.9 ft /sec
