Integration by Parts
Integration by Parts Formula
If $u$ and $v$ are functions of $x$ and have continuous derivatives, then
$
\int u d v=u v-\int v d u
$
Guidelines for Integration by Parts
1. For integrals of the form
$\int x^n e^{a x} d x, \int x^n \sin a x d x$, or $\int x^n \cos a x d x$
let $u=x^n$ and let $d v=e^{a x} d x, \sin a x d x$, or $\cos a x d x$.
2. For integrals of the form
$\int x^n \ln x d x, \int x^n \arcsin a x d x, \int x^n \arccos a x d x$, or $\int x^n \arctan a x d x$ let $u=\ln x, \arcsin a x, \arccos a x$, or $\arctan a x$ and let $d v=x^n d x$.
3. For integrals of the form
$\int e^{a x} \sin b x d x$ or $\int e^{a x} \cos b x d x$
let $u=\sin b x$ or $\cos b x$ and let $d v=e^{a x} d x$.
Example1
- Find $\int x \sin x d x$
▶️Answer/Explanation
Solution
Let $u=x$ and $d v=\sin x d x$.
Then $d u=d x$ and $v=\int \sin x d x=-\cos x$.
$
\begin{aligned}
& \int \stackrel{u}{x} \overbrace{\sin x d x}^{d v}=\stackrel{u}{x} \overbrace{(-\cos x)}^v-\int \overbrace{(-\cos x)}^v \overbrace{d x}^{d u} \\
& =-x \cos x+\int \cos x d x \\
& =-x \cos x+\sin x+C \\
&
\end{aligned}
$
Example 2
- Evaluate $\int \arctan x d x$
▶️Answer/Explanation
Solution
Let $u=\arctan x$ and $d v=d x$.
Then $d u=\frac{1}{1+x^2} d x$ and $v=\int d x=x$
$
\begin{aligned}
& \int \overbrace{\arctan x}^u \overbrace{d x}^{d y}=\overbrace{\arctan x}^u \cdot \overbrace{x}^v-\int \frac{v}{x \cdot} \overbrace{\frac{1}{1+x^2} d x}^{d u} \\
& =x \arctan x-\int \frac{x}{1+x^2} d x \\
& =x \arctan x-\frac{1}{2} \ln \left(1+x^2\right)+C
\end{aligned}
$
Tabular Method
In problems involving repeated applications of integration by parts, a tabular method can help to organized the work. This method works well for integrals of the form $\int x^n e^{a x} d x, \int x^n \sin a x d x$, and $\int x^n \cos a x d x$.
Example 3
- Evaluate $\int x^2 e^x d x$
▶️Answer/Explanation
Solution
Let $u=x^2$ and $d v=e^x d x$.
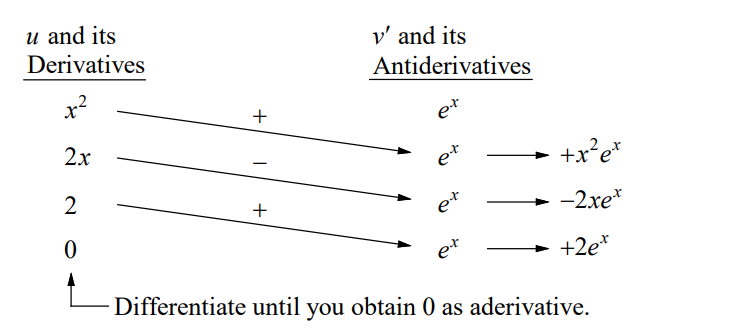
Hence, $\int x^2 e^x d x=x^2 e^x-2 x e^x+2 e^x+C$
Example 4
- Evaluate $\int e^{2 x} \cos x d x$
▶️Answer/Explanation
Solution
Let $u=\cos x$ and $d v=e^{2 x} d x$.
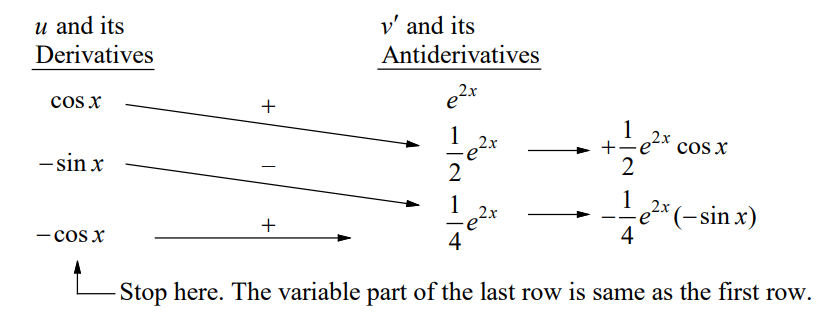
We stop differentiating and integrating as soon as we reach a row that is the same as the first row except for multiplicative constants. The table is interpreted as follow.
$
\int e^{2 x} \cos x d x=\frac{1}{2} e^{2 x} \cos x-\frac{1}{4} e^{2 x}(-\sin x)+\int \overbrace{\frac{1}{4} e^{2 x}(-\cos x)}^{\text {Product of the last row }} d x
$
By adding $\int \frac{1}{4} e^{2 x}(\cos x) d x$ on each side we get,
$
\frac{5}{4} \int e^{2 x} \cos x d x=\frac{1}{2} e^{2 x} \cos x+\frac{1}{4} e^{2 x}(\sin x) .
$
Therefore, $\int e^{2 x} \cos x d x=\frac{2}{5} e^{2 x} \cos x+\frac{1}{5} e^{2 x} \sin x+C$.
Example 5
- $
\int x \sin (2 x) d x=
$
(A) $-x \cos (2 x)+\frac{1}{2} \sin (2 x)+C$
(B) $\frac{x}{2} \cos (2 x)-\frac{1}{4} \sin (2 x)+C$
(C) $-\frac{x}{2} \cos (2 x)+\frac{1}{4} \sin (2 x)+C$
(D) $\frac{x}{2} \cos (2 x)+\frac{1}{4} \sin (2 x)+C$
▶️Answer/Explanation
Ans:C
Example 6
- $
\int_0^2 x e^x d x=
$
(A) $e^2-1$
(B) $e^2+1$
(C) $e-1$
(D) $e+1$
▶️Answer/Explanation
Ans:B
Example 7
- If $\int x^2 \cos (3 x) d x=f(x)-\frac{2}{3} \int x \sin (3 x) d x$, then $f(x)=$
(A) $\frac{2}{3} x \sin (3 x)$
(B) $\frac{1}{3} x^2 \sin (3 x)$
(C) $\frac{2}{3} x \cos (3 x)$
(D) $\frac{1}{3} x \sin (3 x)-\frac{2}{3} \cos (3 x)$
▶️Answer/Explanation
Ans:B
