9.5 The Ratio Test
Ratio Test
Let $\sum a_n$ be a series with nonzero terms.
1. $\sum a_n$ converges absolutely if $\lim _{n \rightarrow \infty}\left|\frac{a_{n+1}}{a_n}\right|<1$.
2. $\sum a_n$ diverges if $\lim _{n \rightarrow \infty}\left|\frac{a_{n+1}}{a_n}\right|>1$ or $\lim _{n \rightarrow \infty}\left|\frac{a_{n+1}}{a_n}\right|=\infty$.
3. The Ratio Test is inconclusive if $\lim _{n \rightarrow \infty}\left|\frac{a_{n+1}}{a_n}\right|=1$.
Example 1
- Determine whether the series is convergent or divergent.
(a) $\sum_{n=1}^{\infty} \frac{3^n}{n !}$
(b) $\sum_{n=1}^{\infty}(-1)^n \frac{n^3}{5^n}$
(c) $\sum_{n=1}^{\infty} \frac{3^n}{2^n-1}$
▶️Answer/Explanation
Solution
(a) $\lim _{n \rightarrow \infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim _{n \rightarrow \infty}\left|\frac{3^{n+1} /(n+1) !}{3^n / n !}\right|=\lim _{n \rightarrow \infty}\left|\frac{3^{n+1}}{(n+1) !} \cdot \frac{n !}{3^n}\right|$
$
=\lim _{n \rightarrow \infty}\left|\frac{3}{n+1}\right|=0<1
$
Thus, by the Ratio Test, the series converges
(b)$
\begin{aligned}
& \lim _{n \rightarrow \infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim _{n \rightarrow \infty}\left|\frac{(-1)^{n+1}(n+1)^3 / 5^{n+1}}{(-1)^n n^3 / 5^n}\right|=\lim _{n \rightarrow \infty} \frac{(n+1)^3}{5^{n+1}} \cdot \frac{5^n}{n^3} \\
& =\lim _{n \rightarrow \infty} \frac{1}{5} \cdot\left(\frac{n+1}{n}\right)^3=\frac{1}{5}<1
\end{aligned}
$
Thus, by the Ratio Test, the series converges.
(c)$
\begin{aligned}
& \lim _{n \rightarrow \infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim _{n \rightarrow \infty}\left|\frac{3^{n+1} /\left(2^{n+1}-1\right)}{3^n /\left(2^n-1\right)}\right|=\lim _{n \rightarrow \infty}\left|\frac{3^{n+1}}{2^{n+1}-1} \cdot \frac{2^n-1}{3^n}\right| \\
& =\lim _{n \rightarrow \infty}\left|\frac{3\left(2^n-1\right)}{2^{n+1}-1}\right|=\lim _{n \rightarrow \infty} \frac{3\left(1-1 / 2^n\right)}{2-1 / 2^n}=\frac{3}{2}>1
\end{aligned}
$
Thus, by the Ratio Test, the series diverges.
Example 2
- Determine whether the series is conditionally convergent or absolute convergent.
(a) $\sum_{n=1}^{\infty}(-1)^n \frac{\sqrt{n}}{n+3}$
(b) $\sum_{n=1}^{\infty} \frac{(-1)^n e^n}{n !}$
▶️Answer/Explanation
Solution
(a)$
\begin{aligned}
& \lim _{n \rightarrow \infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim _{n \rightarrow \infty}\left|\frac{(-1)^{n+1} \sqrt{n+1} /(n+4)}{(-1)^n \sqrt{n} /(n+3)}\right|=\lim _{n \rightarrow \infty} \frac{\sqrt{n+1}}{n+4} \cdot \frac{n+3}{\sqrt{n}} \\
& =\lim _{n \rightarrow \infty} \sqrt{\frac{n+1}{n}} \cdot \frac{n+3}{n+4}=1
\end{aligned}
$
The Ratio Test is in conclusive. Try a different test.
In this case, you can apply the Alternating Series Test.
1. $\lim _{n \rightarrow \infty} a_n=\lim _{n \rightarrow \infty} \frac{\sqrt{n}}{n+3}=0$
2. $a_{n+1}=\frac{\sqrt{n+1}}{(n+1)+3}<\frac{\sqrt{n}}{n+3}=a_n$ for $n \geq 3$
So, the series is conditionally convergent.
(b) $
\begin{aligned}
& \lim _{n \rightarrow \infty}\left|\frac{a_{n+1}}{a_n}\right|=\lim _{n \rightarrow \infty}\left|\frac{e^{n+1} /(n+1) !}{e^n / n !}\right|=\lim _{n \rightarrow \infty}\left|\frac{e^{n+1}}{(n+1) !} \cdot \frac{n !}{e^n}\right| \\
& =\lim _{n \rightarrow \infty} \frac{e}{n+1}=0
\end{aligned}
$
So, the series is absolutely convergent.
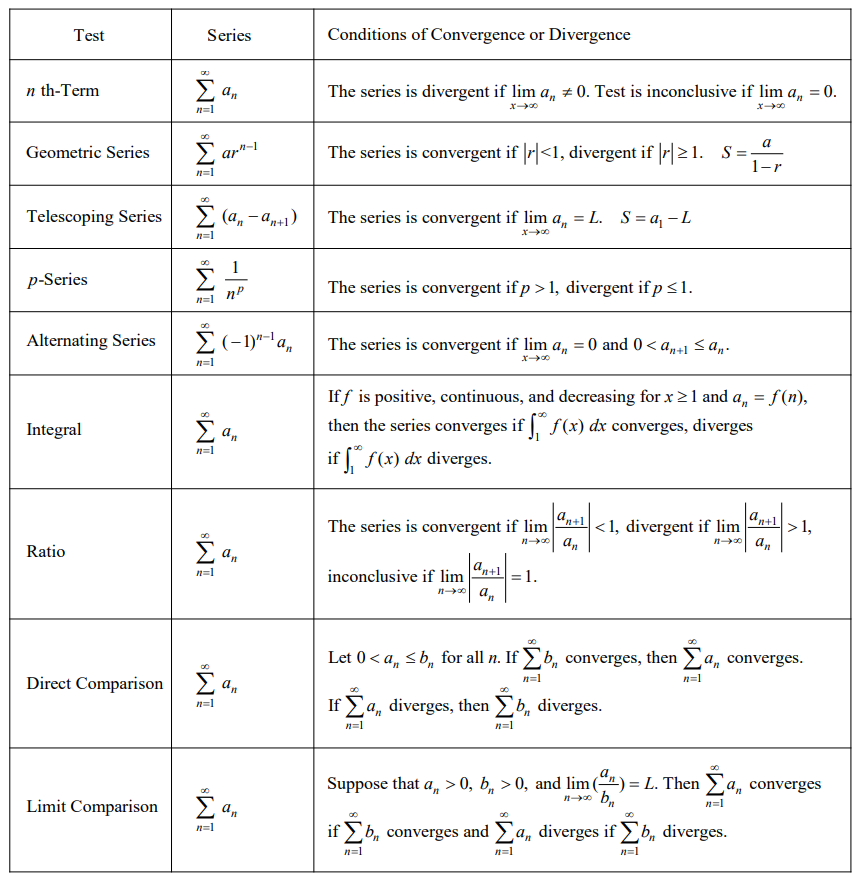
Summary of Tests for Series
Example3
Which of the following series converge?
I. $\sum_{n=1}^{\infty} \frac{n !}{2^n}$
II. $\sum_{n=1}^{\infty} \frac{n}{3^n}$
III. $\sum_{n=1}^{\infty} n\left(\frac{2}{3}\right)^n$
(A) I only
(B) II only
(C) II and III only
(D) I, II, and III
▶️Answer/Explanation
Ans:C
Example4
Which of the following series converge?
I. $\sum_{n=1}^{\infty} \frac{n !}{n^n}$
II. $\sum_{n=1}^{\infty} \frac{(n !)^2}{(2 n) !}$
III. $\sum_{n=1}^{\infty} \frac{n^9}{9^n}$
(A) I only
(B) II only
(C) I and II only
(D) I, II, and III
▶️Answer/Explanation
Ans:D
