8.5 Areas in Polar Coordinates
Area in Polar Coordinates
The area of the region bounded by the graph of $r=f(\theta)$ between the radial lines $\theta=\alpha$ and $\theta=\beta$ is given by
$
\begin{aligned}
\boldsymbol{A} & =\frac{1}{2} \int_\alpha^\beta[\boldsymbol{f}(\theta)]^2 d \theta \\
& =\frac{1}{2} \int_\alpha^\beta \boldsymbol{r}^2 d \theta
\end{aligned}
$
Example 1
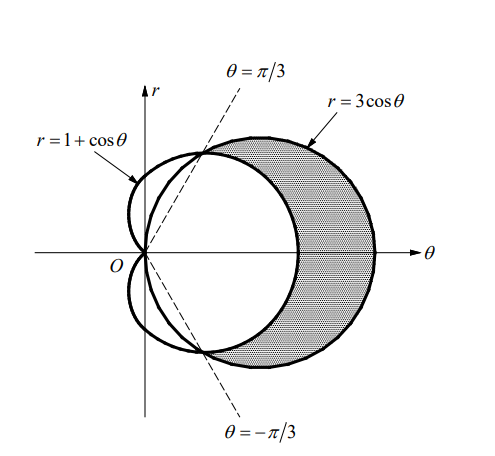
- Find the area of the region that lies inside the circle $r=3 \cos \theta$ and outside the cardioid $r=1+\cos \theta$.
▶️Answer/Explanation
Solution
Find the points of intersection of the two curves.
$
\begin{aligned}
& 3 \cos \theta=1+\cos \theta \\
& \Rightarrow \cos \theta=\frac{1}{2} \Rightarrow \theta= \pm \frac{\pi}{3}
\end{aligned}
$
The desired area can be found by subtracting the area inside the cardioid between $\theta=-\pi / 3$ and $\theta=\pi / 3$ from the area inside the circle between $\theta=-\pi / 3$ and $\theta=\pi / 3$.
$\begin{aligned} A & =\frac{1}{2} \int_\alpha^\beta r^2 d \theta \\ & =\frac{1}{2} \int_{-\pi / 3}^{\pi / 3}\left[(3 \cos \theta)^2-(1+\cos \theta)^2\right] d \theta\end{aligned}$$=2 \cdot \frac{1}{2} \int_0^{\pi / 3}\left[(3 \cos \theta)^2-(1+\cos \theta)^2\right] d \theta$ The region is symmetric about the horizontal axis $\theta=0$
$=\int_0^{\pi / 3}\left[\left(8 \cos ^2 \theta-2 \cos \theta-1\right)\right] d \theta$
$=\int_0^{\pi / 3}\left[8\left(\frac{1+\cos 2 \theta}{2}\right)-2 \cos \theta-1\right] d \theta \quad \cos ^2 \theta=\frac{1+\cos 2 \theta}{2}$
$\begin{aligned} & =\int_0^{\pi / 3}(3+4 \cos 2 \theta-2 \cos \theta) d \theta \\ & =[3 \theta+2 \sin 2 \theta-2 \sin \theta]_0^{\pi / 3} \\ & =\pi+\sqrt{3}-\sqrt{3}=\pi\end{aligned}$
Example 2
The area of the region enclosed by the polar curve $r^2=6 \sin (2 \theta)$ is
(A) 2
(B) 4
(C) 6
(D) 12
▶️Answer/Explanation
Ans:C
Example 3
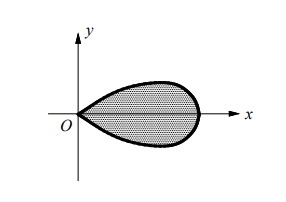
What is the area of the region enclosed by the loop of the graph of the polar curve $r=2 \cos (2 \theta)$ shown in the figure above?
(A) $\frac{\pi}{4}$
(B) $\frac{\pi}{2}$
(C) $\frac{3 \pi}{4}$
(D) $\pi$
▶️Answer/Explanation
Ans:B
Example 4
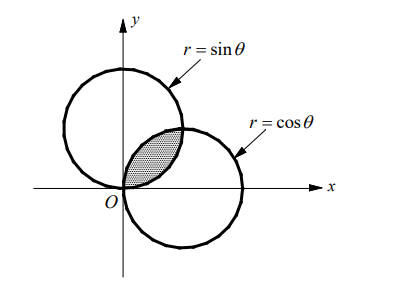
The area of the shaded region that lies inside the polar curves $r=\sin \theta$ and $r=\cos \theta$ is
(A) $\frac{1}{8}(\pi-2)$
(B) $\frac{1}{4}(\pi-2)$
(C) $\frac{1}{2}(\pi-2)$
(D) $\frac{1}{8}(\pi-1)$
▶️Answer/Explanation
Ans:A
Example 5
The area of the region enclosed by the polar curve $r=2+\sin \theta$ is
(A) $3 \pi$
(B) $\frac{7 \pi}{2}$
(C) $4 \pi$
(D) $\frac{9 \pi}{2}$
▶️Answer/Explanation
Ans:D
Example7
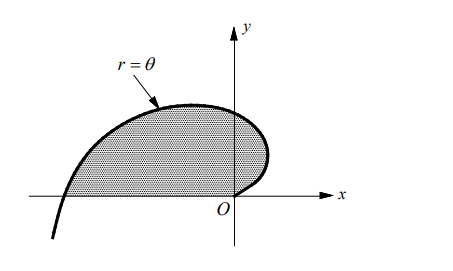
The area of the shaded region bounded by the polar curve $r=\theta$ and the $x$-axis is
(A) $\frac{\pi^2}{4}$
(B) $\frac{\pi^3}{6}$
(C) $\frac{\pi^3}{3}$
(D) $\frac{\pi^3}{2}$
▶️Answer/Explanation
Ans:C
