The slope of the tangent line to the graph of f at the point P(a, f (a)) is the number
\(m=\underset{h\rightarrow 0}{lim}\frac{f\left ( a+h \right )-f\left ( a \right )}{h}\)
if the limit exists.
Recall from the definition of the derivative that this limit is just \({f}’\left ( a \right ).\)
In point slope form the equation of the tangent line is
\(y-f\left ( a \right )={f}’\left ( a \right )\left ( x-a \right )\)
The normal line to the graph of f at the point P(a, f (a)) is the line that passes through P and is perpendicular to the tangent line to the graph of f at P .
Example 1
- Write the equations of the tangent line and normal line to the graph of \(y=x-\frac{x^{2}}{10}\) at the point \(\left ( 4,\frac{12}{5} \right ).\)
▶️Answer/Explanation
Solution
\({y}’=1-\frac{2x}{10}=1-\frac{x}{5}\)
At the point \(\left ( 4,\frac{12}{5} \right )\), the slope is \({y}’|_{x=4}=1-\frac{4}{5}=\frac{1}{5}\) and the equation of tangent line at this point is \(y-\frac{12}{5}=\frac{1}{5}\left ( x-4 \right )\) or \(y=\frac{1}{5}x+\frac{8}{5}.\)
At the point \(\left ( 4,\frac{12}{5} \right )\), the slope e of the normal line is negative reciprocal of 1/5, or -5.
So the equation of normal line at this point is \(y-\frac{12}{5}=-5\left ( x-4 \right )\) or \(y=-5x+22.4.\)
Exercises – Tangent Lines and Normal Lines
Multiple Choice Questions
1. The equation of the line tangent to the graph of \(y=x\sqrt{3+x^{2}}\) at the point (1,2) is
(A) \(y=\frac{3}{2}x-\frac{1}{2}\) (B) \(y=2x+\frac{1}{2}\) (C) \(y=\frac{5}{2}x-\frac{1}{2}\) (D) \(y=\frac{5}{2}x+\frac{1}{2}\)
▶️Answer/Explanation
Ans:
1. C
2. Which of the following is an equation of the line tangent to the graph of \(f\left ( x \right )=x^{2}-x\) at the point where \({f}’\left ( x \right )=3\) ?
(A) \(y=3x-2\)
(B) \(y=3x+2\)
(C) \(y=3x-4\)
(D) \(y=3x+4\)
▶️Answer/Explanation
Ans:
2. C
3. A curve has slope \(2x+x^{-2}\) at each point (x,u) on the curve. Which of the following is an equation for this curve if it passes through the point (1,3) ?
(A) \(y=2x^{2}+\frac{1}{x}\)
(B) \(y=x^{2}-\frac{1}{x}+3\)
(C) \(y=x^{2}+\frac{1}{x}+1\)
(D) \(y=x^{2}-\frac{2}{x^{2}}+4\)
▶️Answer/Explanation
Ans:
3. B
4. An equation of the line normal to the graph of y = tan x, at the point \(\left ( \frac{\pi }{6},\frac{1}{\sqrt{3}} \right )\) is
(A) \(y-\frac{1}{\sqrt{3}}=-\frac{1}{4}\left ( x-\frac{\pi }{6} \right )\)
(B) \(y-\frac{1}{\sqrt{3}}=\frac{1}{4}\left ( x-\frac{\pi }{6} \right )\)
(C) \(y-\frac{1}{\sqrt{3}}=-\frac{3}{4}\left ( x-\frac{\pi }{6} \right )\)
(D) \(y-\frac{1}{\sqrt{3}}=\frac{3}{4}\left ( x-\frac{\pi }{6} \right )\)
▶️Answer/Explanation
Ans:
4. C
5. If \(2x+3y=4\) is an equation of the line normal to the graph of f at the point \(\left ( -1,2 \right )\), then \({f}’\left ( -1 \right )=\)
(A) \(-\frac{2}{3}\) (B) \(\frac{1}{\sqrt{2}}\) (C) \(\sqrt{2}\) (D) \(\frac{3}{2}\)
▶️Answer/Explanation
Ans:
5. D
6. If \(2x-y=k\) is an equation of the line normal to the graph of \(f\left ( x \right )=x^{4}-x\), then k =
(A) \(\frac{23}{16}\) (B) \(\frac{13}{18}\) (C) \(\frac{15}{16}\) (D) \(\frac{9}{8}\)
▶️Answer/Explanation
Ans:
6. A
Free Response Questions
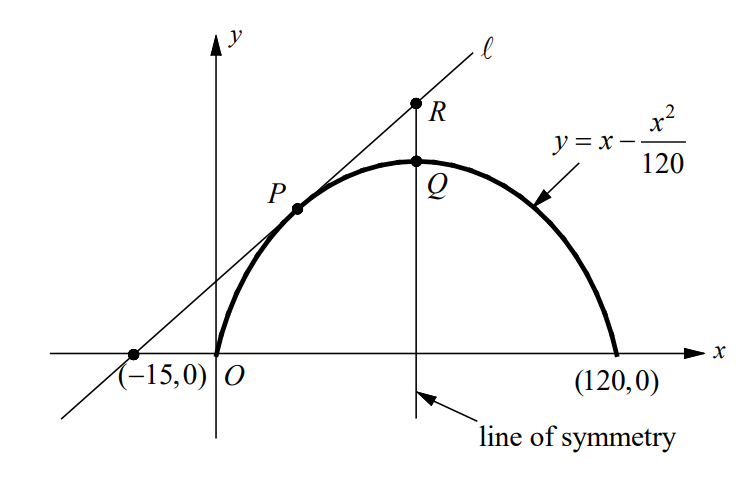
7. Line \(\imath \) is tangent to the graph of \(y=x-\frac{x^{2}}{120}\) at the point P and intersects x-axis at ( 15,0) − as shown in the figure above.
(a) Find the x-coordinates of point P .
(b) Write an equation for line \(\imath \) .
(c) If the line of symmetry for the curve \(y=x-\frac{x^{2}}{120}\) intersects line \(\imath \) at point R , what is the length of \(\bar{QR}\)?
▶️Answer/Explanation
Ans:
7. (a) 30
7. (b) \(y=\frac{1}{2}x+\frac{15}{2}\)
7. (c) 7.5
