7.3 Exponential Growth and Decay
In modeling many real-world situations, a quantity $y$ increases or decreases at a rate proportional to its size at a given time $t$. If $y$ is a function of time $t$, the proportion can be written as follows.
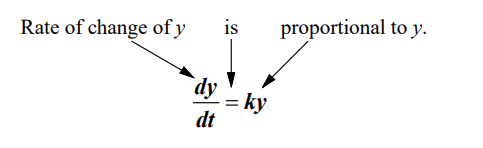
The Law of Exponential Change
If $y$ is a differentiable function of $t$ such that $y>0$ and $y^{\prime}=k y$, for some constant $k$, then
$
\boldsymbol{y}=\boldsymbol{y}_0 \boldsymbol{e}^{\boldsymbol{k t}} \text {, where } y_0 \text { is the initial value of } y .
$
Exponential growth occurs when $k>0$, and exponential decay occurs when $k<0$. The number $k$ is the rate constant of the equation.
Example 1
- The number of bacteria in a culture increases at a rate proportional to the number present. If the number of bacteria was 600 after 3 hours and 19,200 after 8 hours, when will the population reach 120,000 ?
▶️Answer/Explanation
Solution
Since the growth rate is proportional to population size, we use the equation $y=y_0 e^{k t}$.
$
\begin{array}{ll}
600=y_0 e^{k \cdot 3} & y=600 \text { and } t=3 \\
y_0=\frac{600}{e^{3 k}} & \text { Solve for } y_0 \\
19,200=y_0 e^{k \cdot 8} & y=19,200 \text { and } t=8 \\
19,200=\frac{600}{e^{3 k}} e^{8 k} & \text { Substitution } \\
32=e^{5 k} & \text { Simplify. } \\
k=\frac{1}{5} \ln 32 \approx 0.693 &
\end{array}
$
Therefore, the exponential growth model is $y=y_0 e^{0.693 t}$.
To solve for $y_0$, substitute $y=600$ when $t=3$ and obtain
$
\begin{aligned}
& 600=y_0 e^{0.693(3)} . \\
& y_0=\frac{600}{e^{0.693(3)}} \approx 75
\end{aligned}
$
So the model is $y=75 e^{0.693 t}$.
$
\begin{aligned}
& 120,000=75 e^{0.693 t} \Rightarrow \frac{120,000}{75}=e^{0.693 t} \\
& \Rightarrow e^{0.693 t}=1600 \Rightarrow 0.693 t=\ln 1600 \\
& \Rightarrow t \approx 10.646
\end{aligned}
$
Example 2
- Bacteria in a certain culture increase at a rate proportional to the number present. If the number of bacteria doubles every four hours, in how many hours will the number of bacteria triple?
(A) $\ln \left(\frac{27}{2}\right)$
(B) $\ln \left(\frac{81}{2}\right)$
(C) $\frac{4 \ln 2}{\ln 3}$
(D) $\frac{4 \ln 3}{\ln 2}$
▶️Answer/Explanation
Ans:D
Example 3
- Population $y$ grows according to the equation $\frac{d y}{d t}=k y$, where $k$ is a constant and $t$ is measured in years. If the population doubles every 15 years what is the value of $k$ ?
(A) 0.035
(B) 0.046
(C) 0.069
(D) 0.078
▶️Answer/Explanation
Ans:B
Example 4
- A baby weighs 6 pounds at birth and 9 pounds three months later. If the weight of baby increasing at a rate proportional to its weight, then how much will the baby weigh when she is 6 months old?
(A) 11.9
(B) 12.8
(C) 13.5
(D) 14.6
▶️Answer/Explanation
Ans:C
Example 5
- Temperature $F$ changes according to the differential equation $\frac{d F}{d t}=k F$, where $k$ is a constant and $t$ is measured in minutes. If at time $t=0, F=180$ and at time $t=16, F=120$, what is the value of $k$ ?
(A) -0.025
(B) -0.032
(C) -0.045
(D) -0.058
▶️Answer/Explanation
Ans:A
