Integration by Partial Fractions
A method for rewriting a rational function into the sum of simpler rational functions is called the method of partial fractions. For instance, the rational function $\frac{5 x+1}{x^2+x-2}$ can be written
as $\frac{5 x+1}{x^2+x-2}=\frac{2}{x-1}+\frac{3}{x+2}$.
We call the fractions $\frac{2}{x-1}$ and $\frac{3}{x+2}$ partial fractions because their denominators are only part of the original denominator. To integrate the rational function $\frac{5 x+1}{x^2+x-2}$, we simply sum the integrals of the partial fractions.
$
\int \frac{5 x+1}{x^2+x-2} d x=\int \frac{2}{x-1} d x+\int \frac{3}{x+2} d x=2 \ln |x-1|+3 \ln |x+2|+C
$
Example 1
- Evaluate $\int \frac{x^3}{x^2-1} d x$.
▶️Answer/Explanation
Solution
If the degree of the numerator is greater than or equal to the degree of the denominator, divide numerator by the denominator to get a polynomial plus a proper fraction.
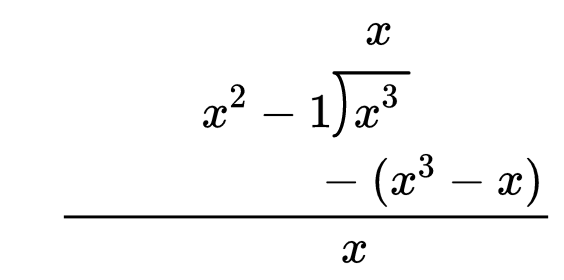
Then we write the improper fraction as a polynomial plus a proper fraction.
$
\frac{x^3}{x^2-1}=x+\frac{x}{x^2-1}
$
Write $\frac{x}{x^2-1}=\frac{x}{(x+1)(x-1)}=\frac{A}{x+1}+\frac{B}{x-1}$.
Multiplying both sides by $(x+1)(x-1)$, we have $x=A(x-1)+B(x+1)$
Let $x=1$. Then $1=A(1-1)+B(1+1) \Rightarrow B=\frac{1}{2}$.
Let $x=-1$. Then $-1=A(-1-1)+B(-1+1) \Rightarrow A=\frac{1}{2}$.
Thus, $\int \frac{x^3}{x^2-1} d x=\int x d x+\frac{1}{2} \int \frac{1}{x+1} d x+\frac{1}{2} \int \frac{1}{x-1} d x$ $=\frac{1}{2} x^2+\frac{1}{2} \ln |x+1|+\frac{1}{2} \ln |x-1|+C$.
Example 2
- Evaluate $\int \frac{x+10}{(x-4)(x+3)} d x$
▶️Answer/Explanation
Solution
If the denominator is a product of distinct linear factors, then the partial fraction decomposition has the form
$
\frac{x+10}{(x-4)(x+3)}=\frac{A}{x-4}+\frac{B}{x+3}
$
To find the values of $A$ and $B$, multiply both sides of the equation by the least common denominator and get $x+10=A(x+3)+B(x-4)$
To solve for $A$, choose $x=4$, to eliminate the term $B(x-4)$.
$
4+10=A(4+3)+B(4-4) \Rightarrow 14=7 A \Rightarrow A=2
$
To solve for $B$, choose $x=-3$, to eliminate the term $A(x+3)$.
$
\begin{aligned}
& -3+10=A(-3+3)+B(-3-4) \Rightarrow 7=-7 B \Rightarrow B=-1 \\
& \int \frac{x+10}{(x-4)(x+3)} d x=\int \frac{2}{(x-4)} d x+\int \frac{-1}{(x+3)} d x \\
& =2 \ln |x-4|-\ln |x+3|+C \\
&
\end{aligned}
$
Example3
- $
\int \frac{d x}{x^2+x-6}=
$
(A) $\frac{1}{5} \ln \left|\frac{x-1}{x+6}\right|+C$
(B) $\frac{1}{5} \ln \left|\frac{x+3}{x-2}\right|+C$
(C) $\frac{1}{5} \ln \left|\frac{x-2}{x+3}\right|+C$
(D) $\frac{1}{5} \ln |(x-2)(x+3)|+C$
▶️Answer/Explanation
Ans:C
Example4
- $
\int_4^7 \frac{5}{(x-2)(2 x+1)} d x=
$
(A) $\ln \frac{9}{10}$
(B) $\ln \frac{10}{9}$
(C) $\ln \frac{3}{2}$
(D) $\ln \frac{9}{4}$
▶️Answer/Explanation
Ans:C
Example5
- $
\int \frac{x}{x^2+5 x+6} d x=
$
(A) $-2 \ln |x+2|+3 \ln |(x+3)|+C$
(B) $2 \ln |x+2|+3 \ln |(x+3)|+C$
(C) $2 \ln |(x+3)|-3 \ln |x+2|+C$
(D) $-2 \ln |(x+3)|-3 \ln |x+2|+C$
▶️Answer/Explanation
Ans:A
Example6
- $
\int \frac{2 e^{2 x}}{\left(e^x-1\right)\left(e^x+1\right)} d x=
$
(A) $\ln \left|e^x\left(e^{2 x}-1\right)\right|+C$
(B) $\ln \left|2 e^x\left(e^{2 x}-1\right)\right|+C$
(C) $\ln \left|\frac{1}{e^{2 x}-1}\right|+C$
(D) $\ln \left|\left(e^x-1\right)\left(e^x+1\right)\right|+C$
▶️Answer/Explanation
Ans:A
