2.7 Implicit Differentiation
The functions that we have met so far have been described by an equation, of the form $y=f(x)$, that expresses $y$ explicitly in terms of $x$ for example, $y=\frac{1}{x^2+1}$ or $y=x+\cos x$. Some functions, however, are defined implicitly by a relation between $x$ and $y$ such as $x^2+4 y^2-9=0$ or $\sin x y=x^2+1$. In some cases it is possible to solve such an equation for $y$ as an explicit function of $x$. But when we are unable to solve for $y$ as a function of $x$, we may still be able to find $\frac{d y}{d x}$ by using the method of implicit differentiation.
Guidelines for Implicit Differentiation
1. Differentiate both sides of the equation with respect to $x$.
2. Collect the terms with $d y / d x$ on the left side of the equation and move all other terms to the right side of the equation.
3. Solve for $d y / d x$.
The tangent line is horizontal if $d y / d x=0$.
The tangent line is vertical when the denominator in the expression for $d y / d x$ is 0 .
Example
- Find $d y / d x$ if $y^2=x^2-\cos x y$
▶️Answer/Explanation
Solution
$\frac{d}{d x}\left(y^2\right)=\frac{d}{d x}\left(x^2\right)-\frac{d}{d x}(\cos x y)$ Differentiate both sides with respect to $x$ treating $y$ as a$
2 y \frac{d y}{d x}=2 x+(\sin x y)\left(x \frac{d y}{d x}+y\right)
$ Treat $x y$ as a product.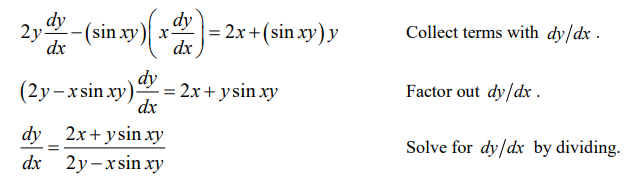
Example
- Consider the curve defined by $x^3+y^3=4 x y+1$.
(a) Find $d y / d x$.
(b) Write an equation for the line tangent to the curve at the point $(2,1)$.
▶️Answer/Explanation
Solution
(a) $3 x^2+3 y^2 \frac{d y}{d x}=4\left(x \frac{d y}{d x}+1 \cdot y\right)$ Differentiate both sides.
$
\begin{aligned}
& 3 x^2+3 y^2 \frac{d y}{d x}=4 x \frac{d y}{d x}+4 y \\
& \frac{d y}{d x}=\frac{4 y-3 x^2}{3 y^2-4 x}
\end{aligned}
$
(b) $\left.\frac{d y}{d x}\right|_{(2,1)}=\frac{4(1)-3(2)^2}{3(1)^2-4(2)}=\frac{8}{5}$
The tangent line is $y-1=\frac{8}{5}(x-2)$ or $y=\frac{8}{5} x-\frac{11}{5}$.
Example
- Consider the curve given by $x^3+y^3-6 x y=0$.
(a) Find $d y / d x$.
(b) Find the $x$-coordinates of each point on the curve where the tangent line is horizontal.
(c) Find the $y$-coordinates of each point on the curve where the tangent line is vertical.
▶️Answer/Explanation
Solution
(a) $3 x^2+3 y^2 \frac{d y}{d x}-6\left(x \frac{d y}{d x}+1 \cdot y\right)=0$ Differentiate both sides.
$
\begin{aligned}
& 3 y^2 \frac{d y}{d x}-6 x \frac{d y}{d x}=6 y-3 x^2 \\
& \frac{d y}{d x}\left(3 y^2-6 x\right)=6 y-3 x^2 \\
& \frac{d y}{d x}=\frac{6 y-3 x^2}{3 y^2-6 x}=\frac{2 y-x^2}{y^2-2 x}
\end{aligned}
$
(b) The tangent line is horizontal when $2 y-x^2=0$. $2 y-x^2=0$ gives $y=1 / 2 x^2$.
Substitute $y=1 / 2 x^2$ to the given equation.
$
\begin{aligned}
& x^3+\left(\frac{1}{2} x^2\right)^3-6 x\left(\frac{1}{2} x^2\right)=0 \Rightarrow \frac{1}{8} x^6-2 x^3=0 \\
& \Rightarrow \frac{1}{8} x^3\left(x^3-16\right)=0 \Rightarrow x=0 \text { or } x=\sqrt[3]{16}
\end{aligned}
$
(c) The tangent line is vertical when $y^2-2 x=0$. $y^2-2 x=0$ gives $x=1 / 2 y^2$.
Substitute $x=1 / 2 y^2$ to the given equation.
$
\begin{aligned}
& \left(\frac{1}{2} y^2\right)^3+y^3-6\left(\frac{1}{2} y^2\right) y=0 \Rightarrow \frac{1}{8} y^6-2 y^3=0 \\
& \Rightarrow \frac{1}{8} y^3\left(y^3-16\right)=0 \Rightarrow y=0 \text { or } y=\sqrt[3]{16}
\end{aligned}
$
Exercises – Implicit Differentiation
Multiple Choice Questions
- 1. If $3 x y+x^2-2 y^2=2$, then the value of $\frac{d y}{d x}$ at the point $(1,1)$ is
(A) 5
(B) $\frac{7}{2}$
(C) $-\frac{1}{2}$
(D) $-\frac{7}{2}$
▶️Answer/Explanation
Ans:A
Example
2. If $3 x^4-x^2-y^2=0$, then the value of $\frac{d y}{d x}$ at the point $(1, \sqrt{2})$ is
(A) $\frac{\sqrt{2}}{2}$
(B) $\frac{3 \sqrt{2}}{2}$
(C) $\frac{5 \sqrt{2}}{2}$
(D) $\frac{7 \sqrt{2}}{2}$
▶️Answer/Explanation
Ans:C
Example
- 3. If $x^2 y+2 x y^2=5 x$, then $\frac{d y}{d x}=$
(A) $\frac{5-4 x y-4 y}{x^2+4 x y}$
(B) $\frac{5-2 x y-2 y^2}{x^2+4 x y}$
(C) $\frac{5-2 x y-y^2}{x^2+2 x y}$
(D) $\frac{5-x y-2 y}{x^2-2 x y}$
▶️Answer/Explanation
Ans:B
Example
- If $x y+\tan (x y)=\pi$, then $\frac{d y}{d x}=$
(A) $-y \sec ^2(x y)$
(B) $-y \cos ^2(x y)$
(C) $-x \sec ^2(x y)$
(D) $-\frac{y}{x}$
▶️Answer/Explanation
Ans:D
