Motion of a Particle, Distance, and Displacement
If a particle moves along a straight line with position function $s(t)$, then its velocity is $v(t)=s^{\prime}(t)$, so
$
s(b)-s(a)=\int_a^b v(t) d t
$
is the change of the position, or displacement, of the particle during the time period from $t=a$ to $t=b$.
The average velocity and the average acceleration over the time interval from $t=a$ to $t=b$ is
Average velocity $=\frac{\text { displacement }}{\text { time }}=\frac{s(b)-s(a)}{b-a}=\frac{1}{b-a} \int_a^b v(t) d t$
Average acceleration $=\frac{v(b)-v(a)}{b-a}=\frac{1}{b-a} \int_a^b a(t) d t$
To find the total distance traveled we have to consider when the particle moves to the right, $v(t) \geq 0$, and when the particle moves to the left, $v(t) \leq 0$.
In both cases, the distance is computed by integrating $|v(t)|$, the speed of the particle. Therefore
Total distance traveled $=\int_a^b|v(t)| d t$
Average speed $=\frac{\text { distance traveled }}{\text { time }}=\frac{1}{b-a} \int_a^b|v(t)| d t$.
The acceleration of the object is $a(t)=v^{\prime}(t)$, so
$
v(b)-v(a)=\int_a^b a(t) d t
$
is the change in velocity from $t=a$ to $t=b$.
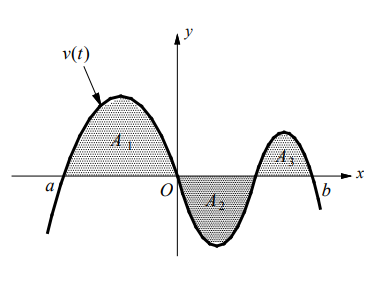
The figure at the right shows how both displacement and distance traveled can be interpreted in terms of areas under a velocity curve.
displacement
$
=\int_a^b v(t) d t=A_1-A_{\mathbf{2}}+A_3
$
total distance traveled
$
=\int_a^b|v(t)| d t=A_1+A_2+A_3
$
Example 1
- A particle moves along the $x$-axis so that its velocity at any time $t \geq 0$ is given by $v(t)=t^2-3 t-4$.
(a) In which direction (left or right) is the particle moving at time $t=5$ ?
(b) Find the acceleration of the particle at time $t=5$.
(c) Given that $x(t)$ is the position of the particle at time $t$ and that $x(0)=12$, find $x(3)$.
(d) Find the total distance traveled by the particle from $t=0$ to $t=6$.
(e) Find the average speed of the particle from $t=0$ to $t=6$.
(f) For what values of $t, 0 \leq t \leq 6$, is the particle’s instantaneous velocity the same as its average velocity on the closed interval $[0,6]$ ?
▶️Answer/Explanation
Solution
(a) $v(5)=(5)^2-3(5)-4>0$
Since $v(5)>0$, particle is moving to the right.
(b) $a(t)=v^{\prime}(t)=2 t-3$ So $a(5)=2(5)-3=7$.
(c) $\begin{aligned} & x(3)-x(0)=\int_0^3 v(t) d t=\int_0^3\left(t^2-3 t-4\right) d t \\ = & {\left[\frac{1}{3} t^3-\frac{3}{2} t^2-4 t\right]_0^3=-16.5 } \\ & x(3)=x(0)-16.5=12-16.5=-4.5\end{aligned}$
$\begin{aligned} & \text { (d) Total distance traveled }=\int_a^b|v(t)| d t=\int_0^6\left|t^2-3 t-4\right| d t \\ & =-\int_0^4\left(t^2-3 t-4\right) d t+\int_4^6\left(t^2-3 t-4\right) d t=\frac{56}{3}+\frac{38}{3}=\frac{94}{3}\end{aligned}$
(e) Average speed $=\frac{\text { distance traveled }}{\text { time }}=\frac{94 / 3}{6}=\frac{47}{9}$
$\begin{aligned} & \text { (f) Average velocity }=\frac{\text { displacement }}{\text { time }}=\frac{x(6)-x(0)}{6-0} \\ & =\frac{\int_0^6\left(t^2-3 t-4\right) d t}{6}=\frac{-6}{6}=-1 \\ & t^2-3 t-4=-1 \Rightarrow t^2-3 t-3=0 \quad \text { Since } t \geq 0, t=\frac{3+\sqrt{21}}{2} .\end{aligned}$
Example 2
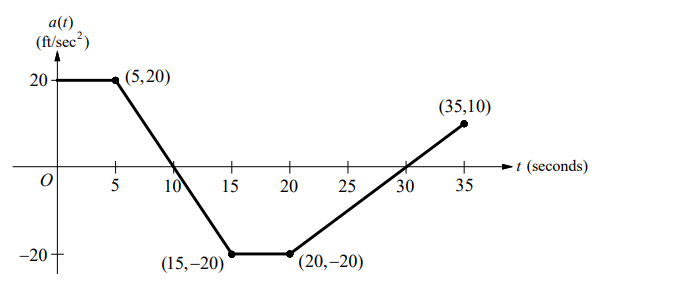
A car is traveling on a straight road with velocity $80 \mathrm{ft} / \mathrm{sec}$ at time $t=0$. For $0 \leq t \leq 35$ seconds, the cars acceleration $a(t)$, in $\mathrm{ft} / \mathrm{sec}^2$, is the piecewise linear function defined by the graph above.
(a) Find $a(15)$ and $v(15)$.
(b) At what time, other than $t=0$, on the interval $0 \leq t \leq 35$, is the velocity of the car $80 \mathrm{ft} / \mathrm{sec}$ ?
(c) On the time interval $0 \leq t \leq 35$, what is the car’s absolute maximum velocity, in $\mathrm{ft} / \mathrm{sec}$, and at what time does it occur?
(d) On the time interval $0 \leq t \leq 35$, what is the car’s absolute minimum velocity, in $\mathrm{ft} / \mathrm{sec}$, and at what time does it occur?
▶️Answer/Explanation
Solution
(a) $a(15)=-20$
$
\begin{aligned}
& v(15)=v(0)+\int_0^{15} a(t) d t \\
& =v(0)+\int_0^{10} a(t) d t+\int_{10}^{15} a(t) d t \\
& =80+\frac{1}{2}(10+5) \cdot 20-\frac{1}{2}(5)(20) \\
& =180
\end{aligned}
$
$
v(0)=80
$
(b) At time $t=20$. Because the area above the $x$-axis from $t=0$ to $t=10$ is same as the area below the $x$-axis from $t=10$ to $t=20$.
(c) Check endpoints and the points where $a(t)$ changes signs.
$
\begin{aligned}
v(0) & =80 \\
v(10) & =v(0)+\int_0^{10} a(t) d t \quad \text { When } t=10, a(t) \text { changes signs. } \\
& =80+\frac{1}{2}(10+5) \cdot 20=230 \\
v(30) & =v(0)+\int_0^{30} a(t) d t \\
& =80+\frac{1}{2}(10+5) \cdot 20-\frac{1}{2}(20+5) \cdot 20 \quad \text { When } t=30, a(t) \text { changes signs. } \\
& =-20 \\
v(35) & =v(0)+\int_0^{35} a(t) d t \\
& =80+\frac{1}{2}(10+5) \cdot 20-\frac{1}{2}(20+5) \cdot 20+\frac{1}{2}(5)(10) \\
& =5
\end{aligned}
$
The car’s absolute maximum velocity is $230 \mathrm{ft} / \mathrm{sec}$ and it occurs at $t=10$.
(d) The car’s absolute minimum velocity is $-20 \mathrm{ft} / \mathrm{sec}$ and it occurs at $t=30$.
Example 3
- The acceleration of a particle moving along the $x$-axis at time $t$ is given by $a(t)=2 t-6$.
If at $t=1$, the velocity of the particle is 3 and its position is $\frac{1}{3}$, then the position $x(t)=$
(A) $\frac{t^3}{3}-6 t^2+5 t+\frac{1}{3}$
(B) $\frac{t^3}{3}-3 t^2+8 t-5$
(C) $\frac{t^3}{3}-6 t+9$
(D) $\frac{t^3}{3}-3 t^2+8 t-\frac{7}{3}$
▶️Answer/Explanation
Ans:B
Example 4
- The velocity of a particle moving along the $x$-axis at any time $t$ is given by $v(t)=3 e^{-t}-t$. What is the average speed of the particle over the time interval $0 \leq t \leq 3$ ?
(A) 0.873
(B) 1.096
(C) 1.273
(D) 1.482
▶️Answer/Explanation
Ans:D
Example 5
- A particle travels along a straight line with a velocity of $v(t)=e^t\left(t^2-5 t+6\right)$ meters per second. What is the average velocity of the particle over the time interval $0 \leq t \leq 5$ ?
(A) 58.602
(B) 64.206
(C) 79.351
(D) 86.448
▶️Answer/Explanation
Ans:D