Area of a Region Between Two Curves
Area of a Region Between Two Curves
If $f$ and $g$ are continuous on $[a, b]$ and $g(x) \leq f(x)$ for all $x$ on $[a, b]$, then the area of the region bounded by the graphs of $f$ and $g$ and the vertical lines $x=a$ and $x=b$ is
$
A=\int_a^b[f(x)-g(x)] d x
$
In general, to determine the area between two curves, we can use
$
A=\int_{x_1}^{x_2}[(\text { top curve) }-(\text { bottom curve })] d x
$
if the curves are defined by functions of $x$, and
$
A=\int_{y_1}^{y_2}[(\text { right curve })-(\text { left curve })] d y,
$
if the curves are defined by functions of $y$.
- Example 1
Find the area of the region in the first quadrant enclosed by the graphs of $f(x)=2 \cos x, g(x)=x$ and the $y$-axis.
▶️Answer/Explanation
Solution
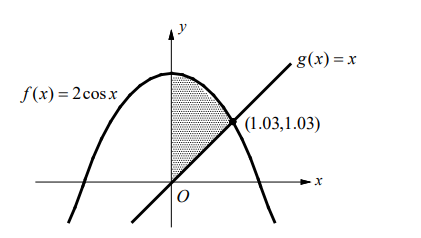
The limits of integration are $a=0$ and $b=1.03$.
Use a graphing calculator to find the point of intersection and sketch the two curves. The point of intersection in the first quadrant is $(1.03,1.03)$.
The area between the curves is
$
\begin{aligned}
A & =\int_a^b[f(x)-g(x)] d x \\
& =\int_0^{1.03}[2 \cos x-x] d x \\
& =\left[2 \sin x-\frac{x^2}{2}\right]_0^{1.03} \\
& =\left(2 \sin 1.03-\frac{1.03^2}{2}\right)-(2 \sin 0-0) \\
& =1.184
\end{aligned}
$
Example 2
- What is the area of the region enclosed by the graphs of $f(x)=x+2$ and $g(x)=x^3-4 x^2+6$ ?
(A) $\frac{193}{12}$
(B) $\frac{218}{12}$
(C) $\frac{253}{12}$
(D) $\frac{305}{12}$
▶️Answer/Explanation
Ans:C
Example 3
- What is the area of the region in the first quadrant, bounded by the curve $y=\sqrt[3]{x}$ and $y=x$ ?
(A) $\frac{1}{5}$
(B) $\frac{1}{4}$
(C) $\frac{1}{3}$
(D) $\frac{1}{2}$
▶️Answer/Explanation
Ans:B
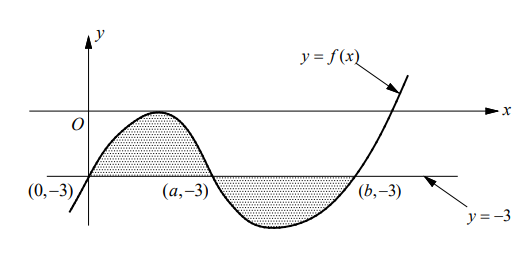
Example5
The curve $y=f(x)$ and the line $y=-3$, shown in the figure above, intersect at the points $(0,-3)$, $(a,-3)$, and $(b,-3)$. The sum of area of the shaded region enclosed by the curve and the line is given by
(A) $\int_0^a[3-f(x)] d x+\int_a^b[-3+f(x)] d x$
(B) $\int_0^a[-3+f(x)] d x+\int_a^b[3-f(x)] d x$
(C) $\int_0^a[f(x)+3] d x+\int_a^b[-3-f(x)] d x$
(D) $\int_0^a[f(x)-3] d x+\int_a^b[3-f(x)] d x$
▶️Answer/Explanation
Ans:C