The statement \(\underset{x\rightarrow c}{lim}f\left ( x \right )=\infty \) means that f (x) approaches infinity as x approaches c.
The statement \(\underset{x\rightarrow c}{lim}f\left ( x \right )=\infty \) means that f (x) approaches negative infinity as x approaches c.
Definition of Vertical Asymptote
If f (x) approaches infinity (or negative infinity) as x approaches c from the right or the left, then the line x = c is a vertical asymptote of the graph of f.
The graph of rational function given by \(y=\frac{f\left ( x \right )}{g\left ( x \right )}\) has a vertical asymptote at x = c if \(g\left ( c \right )=0\) and \(f\left ( c \right )\neq 0\).
Definition of Horizontal Asymptote
A line y = b is a horizontal asymptote of the graph of a function y = f (x) if either
\(\underset{x\rightarrow \infty}{lim}f\left ( x \right )=b\) or \(\underset{x\rightarrow -\infty}{lim}f\left ( x \right )=b\).
The statement \(\underset{x\rightarrow \infty}{lim}f\left ( x \right )=L\) means that f (x) has the limit L as x approaches infinity.
The statement \(\underset{x\rightarrow -\infty}{lim}f\left ( x \right )=L\) means that f (x) has the limit L as x approaches negative infinity.
Example 1
- Find all vertical asymptotes of the graph of each function.
(a) \(f\left ( x \right )=\frac{x}{x^{2}-1}\)
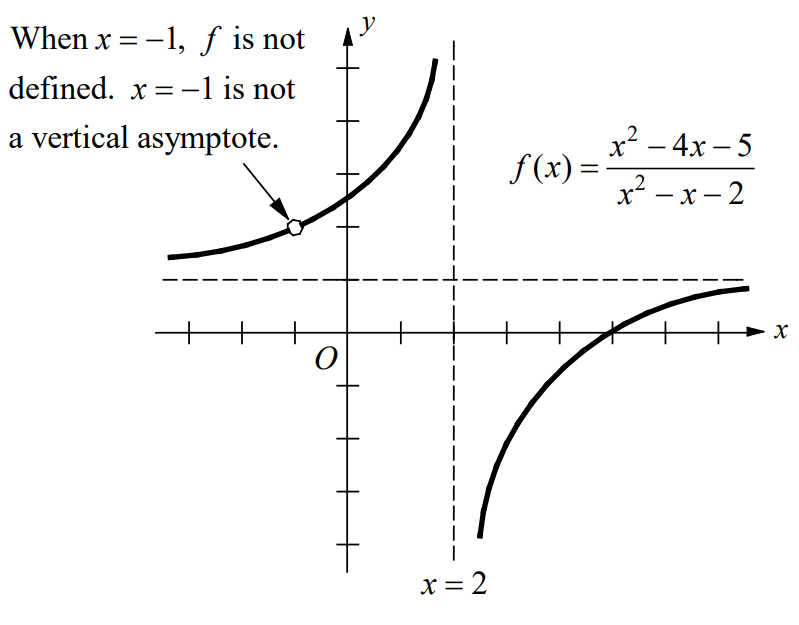
(b) \(f\left ( x \right )=\frac{x^{2}-4x-5}{x^{2}-x-2}\)
▶️Answer/Explanation
Solution
(a) \(f\left ( x \right )=\frac{x}{x^{2}-1}\)
\(\frac{x}{\left ( x+1 \right )\left ( x-1 \right )}\)
Factor the denominator.
The denominator is 0 at x = −1 and x = 1 . The numerator is not 0 at these two points. There are two vertical asymptotes, x = −1 and x = 1 .
(b)

At all values other than x = −1, the graph of f coincides with the graph of \(y=\left ( x-5 \right )/\left ( x-2 \right ).\) So, x = 2 is the only vertical asymptote. At x = −1 the graph is not continuous.
The statement \(\underset{x\rightarrow c}{lim}f\left ( x \right )=\infty \) means that f (x) approaches infinity as x approaches c.
The statement \(\underset{x\rightarrow c}{lim}f\left ( x \right )=\infty \) means that f (x) approaches negative infinity as x approaches c.
Definition of Vertical Asymptote
If f (x) approaches infinity (or negative infinity) as x approaches c from the right or the left, then the line x = c is a vertical asymptote of the graph of f.
The graph of rational function given by \(y=\frac{f\left ( x \right )}{g\left ( x \right )}\) has a vertical asymptote at x = c if \(g\left ( c \right )=0\) and \(f\left ( c \right )\neq 0\).
Definition of Horizontal Asymptote
A line y = b is a horizontal asymptote of the graph of a function y = f (x) if either
\(\underset{x\rightarrow \infty}{lim}f\left ( x \right )=b\) or \(\underset{x\rightarrow -\infty}{lim}f\left ( x \right )=b\).
The statement \(\underset{x\rightarrow \infty}{lim}f\left ( x \right )=L\) means that f (x) has the limit L as x approaches infinity.
The statement \(\underset{x\rightarrow -\infty}{lim}f\left ( x \right )=L\) means that f (x) has the limit L as x approaches negative infinity.
Example 1
- Find all vertical asymptotes of the graph of each function.
(a) \(f\left ( x \right )=\frac{x}{x^{2}-1}\)
(b) \(f\left ( x \right )=\frac{x^{2}-4x-5}{x^{2}-x-2}\)
▶️Answer/Explanation
Solution
(a) \(f\left ( x \right )=\frac{x}{x^{2}-1}\)
\(\frac{x}{\left ( x+1 \right )\left ( x-1 \right )}\)
Factor the denominator.
The denominator is 0 at x = −1 and x = 1 . The numerator is not 0 at these two points. There are two vertical asymptotes, x = −1 and x = 1 .
(b)

At all values other than x = −1, the graph of f coincides with the graph of \(y=\left ( x-5 \right )/\left ( x-2 \right ).\) So, x = 2 is the only vertical asymptote. At x = −1 the graph is not continuous.

Example 2
- Find the limit.
(a) \(\underset{x\rightarrow \infty }{lim}\frac{x^{3}-4x^{2}+7}{2x^{3}-3x-5}\)
(b) \(\underset{x\rightarrow \infty }{lim}\frac{\sqrt{4x^{2}+6x}}{3x-2}\)
▶️Answer/Explanation
Solution
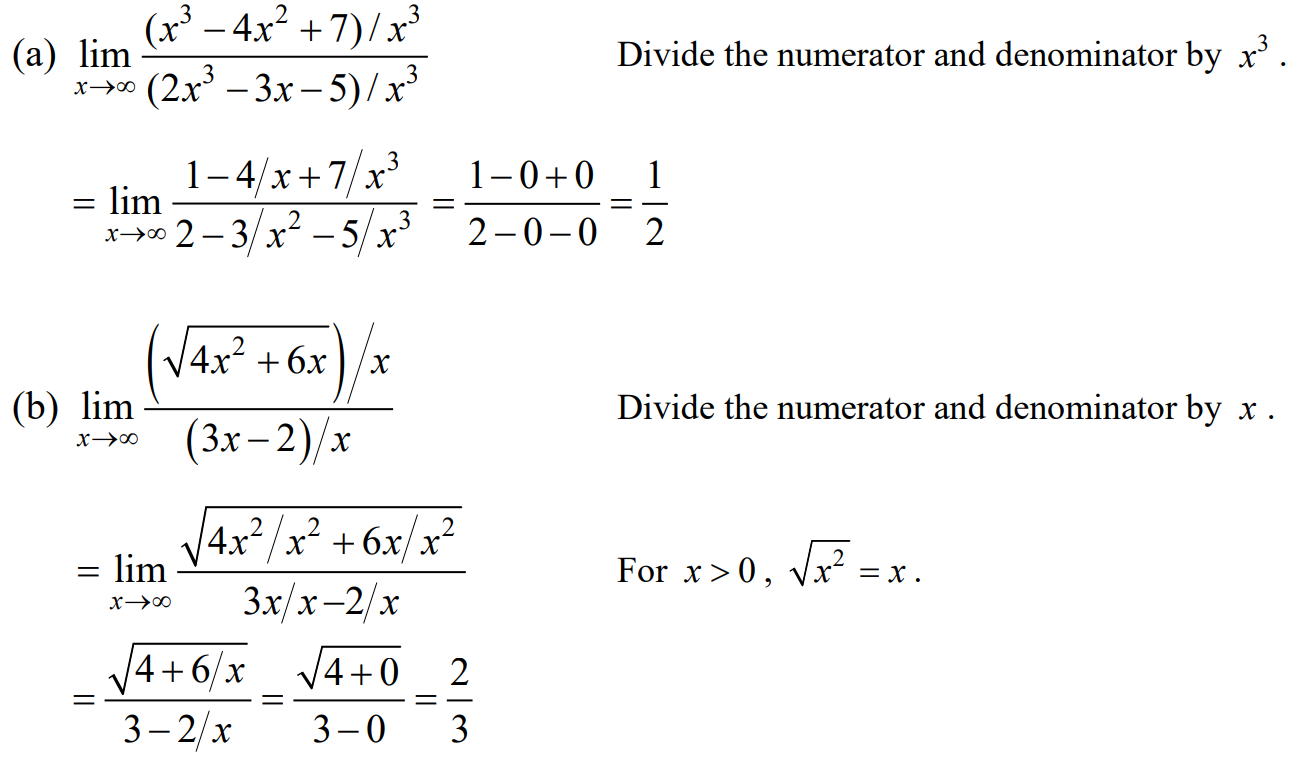
Example 3
- Find the horizontal asymptotes of the graph of the function \(f\left ( x \right )=\frac{\sqrt[3]{2x^{3}-9}}{x}\).
▶️Answer/Explanation
Solution

Exercises – Limits and Asymptotes
Multiple Choice Questions
Question
- \(\underset{x\rightarrow \infty }{lim}\frac{3+2x^{2}-x^{4}}{3x^{4}-5}=\)
(A) -2 (B) \(-\frac{1}{3}\) (C) \(\frac{1}{5}\) (D) 1
▶️Answer/Explanation
Ans:
1. B
Question
- What is \(\underset{x\rightarrow \infty }{lim}\frac{x^{3}+x-8}{2x^{3}+3x-1}=\)
(A) \(-\frac{1}{2}\) (B) 0 (C) \(\frac{1}{2}\) (D) 2
▶️Answer/Explanation
Ans:
2. C
Question
- Which of the following lines is an asymptote of the graph of \(f\left ( x \right )=\frac{x^{2}+5x+6}{x^{2}-x-12}?\)
I. x = −3
II. x = 4
III. y = 1
(A) II only (B) III only (C) II and III only (D) I, II, and III
▶️Answer/Explanation
Ans:
3. C
Question
- If the horizontal line y = 1 is an asymptote for the graph of the function f , which of the following statements must be true?
(A) \(\underset{x\rightarrow \infty }{lim}f\left ( x \right )=1\)
(B) \(\underset{x\rightarrow 1}{lim}f\left ( x \right )=\infty\)
(C) f (1) is undefined
(D) f (x) = 1 for all x
▶️Answer/Explanation
Ans:
4. A
Question
- If x = 1 is the vertical asymptote and y = −3 is the horizontal asymptote for the graph of the function f , which of the following could be the equation of the curve?
(A) \(f\left ( x \right )=\frac{-3x^{2}}{x-1}\)
(B) \(f\left ( x \right )=\frac{-3\left ( x-1 \right )}{x+3}\)
(C) \(f\left ( x \right )=\frac{-3\left ( x^{2}-1 \right )}{x-1}\)
(D) \(f\left ( x \right )=\frac{-3\left ( x^{2}-1 \right )}{\left (x-1 \right )^{2}}\)
▶️Answer/Explanation
Ans:
5. D
Question
- What are all horizontal asymptotes of the graph of \(y=\frac{6+3e^{x}}{3-3e^{x}}\) in the xy – plane?
(A) y = −1 only
(B) y = 2 only
(C) y = −1 and y = 2
(D) y = 0 and y = 2
▶️Answer/Explanation
Ans:
6. C
Question
- Let \(f\left ( x \right )=\frac{3x-1}{x^{3}-8}.\)
(A) Find the vertical asymptote(s) of f . Show the work that leads to your answer.
(B) Find the horizontal asymptote(s) of f . Show the work that leads to your answer.
▶️Answer/Explanation
Ans:
7. (a) x = 2
(b) y = 0
Question
- Let \(f\left ( x \right )=\frac{sin x}{x^{2}+2x}.\)
(A) Find the vertical asymptote(s) of f . Show the work that leads to your answer.
(B) Find the horizontal asymptote(s) of f . Show the work that leads to your answer.
▶️Answer/Explanation
Ans:
8. (a) x = −2
(b) y = 0
