Rolle’s Theorem and The Mean Value Theorem
Rolle’s Theorem
Let $f$ be continuous on the closed interval $[a, b]$ and differentiable on the open interval $(a, b)$. If $f(a)=f(b)$, then there is at least one number $c$ in the open interval $(a, b)$ such that
$
f^{\prime}(c)=0
$
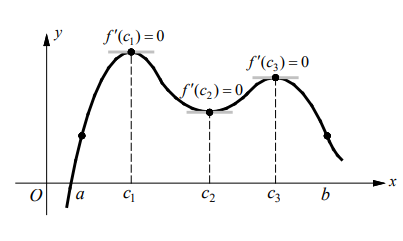
Rolle’s Theorem says that a differentiable curve has at least one horizontal tangent between $a$ and $b$ if $f(a)=f(b)$.
The Mean Value Theorem
If $f$ is continuous on the closed interval $[a, b]$ and differentiable on the open interval $(a, b)$, then there exists a number $c$ in the open interval $(a, b)$ such that
$
f^{\prime}(c)=\frac{f(b)-f(a)}{b-a}
$
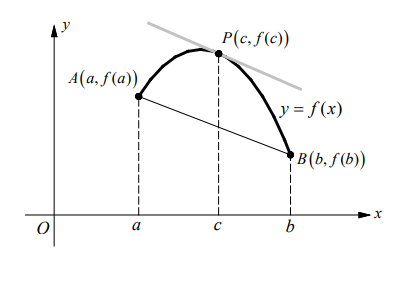
The Mean Value Theorem says that there is at least one point $P(c, f(c))$, on the curve where the tangent line is parallel to the secant line $A B$.
Example
- Let $f$ be the function given by $f(x)=x^3-9 x+1$. Find all numbers $c$ that satisfies the conclusion of Rolle’s Theorem for $f$, such that $f^{\prime}(c)=0$ on the closed interval $[0,3]$.
▶️Answer/Explanation
Solution
$
\begin{aligned}
& f(x)=x^3-9 x+1 \\
& f(0)=1 \\
& f(3)=(3)^3-9(3)+1=1
\end{aligned}
$
So, $f(0)=f(3)$, and from Rolle’s Theorem there exists at least one number $c$ in the open interval $(0,3)$ such that $f^{\prime}(c)=0$.
$
\begin{aligned}
& f^{\prime}(x)=3 x^2-9 \\
& f^{\prime}(c)=3 c^2-9=0 \\
& c^2=3 \Rightarrow c= \pm \sqrt{3}
\end{aligned}
$
Differentiate.
Set $f^{\prime}(c)$ equal to 0 .
But $-\sqrt{3}$ is not in $(0,3)$, so $c=\sqrt{3}$.
Example
- Let $f$ be the function given by $f(x)=x^3-2 x^2+x-5$.
Find all numbers $c$ that satisfy the conclusion of the
Mean Value Theorem for $f$ on the closed interval $[-1,2]$.
▶️Answer/Explanation
Solution
$\begin{array}{ll}f(x)=x^3-2 x^2+x-5 & \\ f^{\prime}(x)=3 x^2-4 x+1 & \text { Differentiate. } \\ f^{\prime}(c)=3 c^2-4 c+1 & \\ f(2)=(2)^3-2(2)^2+2-5=-3 & \\ f(-1)=(-1)^3-2(-1)^2-1-5=-9 & \text { Mean Value Theorem } \\ f^{\prime}(c)=\frac{f(b)-f(a)}{b-a} & \quad b=2 \text { and } a=-1 \\ 3 c^2-4 c+1=\frac{f(2)-f(-1)}{2-(-1)} & \\ 3 c^2-4 c+1=\frac{-3+9}{2+1} & \text { Simplify. } \\ 3 c^2-4 c-1=0 & \\ c=\frac{2 \pm \sqrt{7}}{3} & \\ c=\frac{2+\sqrt{7}}{3} \approx 1.549 \text { and } c=\frac{2-\sqrt{7}}{3} \approx-.215 & \end{array}$
Both numbers lie in the open interval $(-1,2)$, so $\frac{2 \pm \sqrt{7}}{3}$ satisfy the conclusion of the Mean Value Theorem.
Exercises – Roll’s Theorem and the Mean Value Theorem
Multiple Choice Questions
1. Let $f$ be the function given by $f(x)=\sin (\pi x)$. What are the values of $c$ that satisfy Roll’s Theorem on the closed interval $[0,2]$ ?
(A) $\frac{1}{4}$ only
(B) $\frac{1}{2}$ only
(C) $\frac{1}{4}$ and $\frac{1}{2}$
(D) $\frac{1}{2}$ and $\frac{3}{2}$
▶️Answer/Explanation
Ans:D
Question
- Let $f$ be the function given by $f(x)=-x^3+3 x+2$. What are the values of $c$ that satisfy Mean Value Theorem on the closed interval $[0,3]$ ?
(A) $-\sqrt{3}$ only
(B) $-\sqrt{3}$ and $\sqrt{3}$
(C) $\sqrt{3}$ only
(D) 1.5 and $\sqrt{3}$
▶️Answer/Explanation
Ans:C
Question
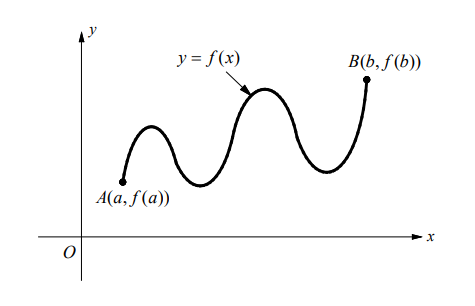
- The figure above shows the graph of $f$. On the closed interval $[a, b]$, how many values of $c$ satisfy the conclusion of the Mean Value Theorem?
(A) 2
(B) 3
(C) 4
(D) 5
▶️Answer/Explanation
Ans:C
Question
- Let $f$ be the function given by $f(x)=\frac{x}{x+2}$. What are the values of $c$ that satisfy the Mean Value Theorem on the closed interval $[-1,2]$ ?
(A) -4 only
(B) 0 only
(C) 0 and $\frac{3}{2}$
(D) -4 and 0
▶️Answer/Explanation
Ans:B
