Volumes by Disk and Washers
The solid generated by rotating a plane region about an axis is called a solid of revolution.
The simplest such solid is a right circular cylinder or disk.
Volume of disk = (base area of disk)(width of disk)
$\Delta V=A(x) \Delta x$.
So the definition of volume gives us $V=\int_a^b A(x) d x$.
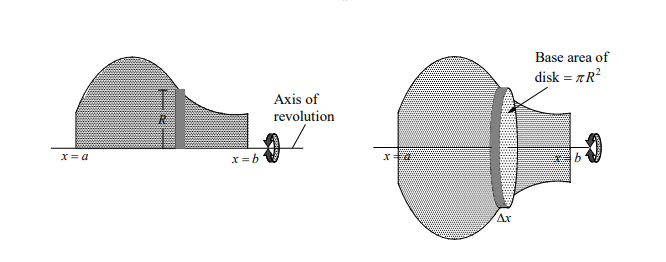
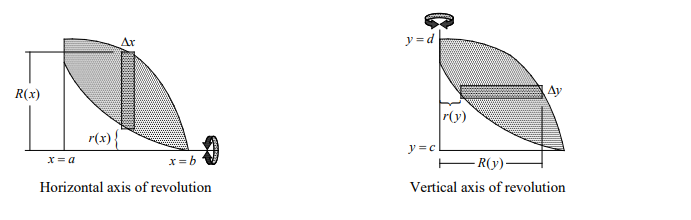
The Disk Method
Horizontal Axis of Revolution Vertical Axis of Revolution
$
V=\pi \int_a^b[R(x)]^2 d x \quad\quad \quad V=\pi \int_{\mathrm{c}}^{\mathrm{d}}[R(y)]^2 d y
$

The Washer Method
Horizontal Axis of Revolution Vertical Axis of Revolution
$V=\pi \int_a^b\left([R(x)]^2-[r(x)]^2\right) d x \quad V=\pi \int_c^d\left([R(y)]^2-[r(y)]^2\right) d y$
Example 2
- Find the volume of the solid generated by revolving the region bounded by the graphs of $y=\sqrt{x}, x=1$, and $x=4$ about the $x$-axis.
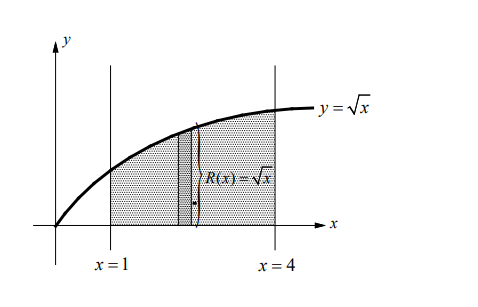
▶️Answer/Explanation
Solution
Sketch the graphs. The volume is
$
\begin{aligned}
V & =\pi \int_a^b[R(x)]^2 d x \\
& =\pi \int_1^4[\sqrt{x}]^2 d x=\pi \int_1^4 x d x \\
& =\pi\left[\frac{x^2}{2}\right]_1^4=\pi\left(\frac{16}{2}-\frac{1}{2}\right) \\
& =\frac{15 \pi}{2}
\end{aligned}
$
Example 3
- The region in the first quadrant bounded by the graph of $y=\sec x, x=\frac{\pi}{3}$, and the coordinate axes is rotated about the $x$-axis. What is the volume of the solid generated?
(A) $\frac{\pi}{3}$
(B) $\frac{\pi}{2}$
(C) $\sqrt{3} \pi$
(D) $3 \pi$
▶️Answer/Explanation
Ans:C
Example 4
- The region enclosed by the graphs of $y=e^{(x / 2)}$ and $y=(x-1)^2$ from $x=0$ to $x=1$ is rotated about the $x$-axis. What is the volume of the solid generated?
(A) $\frac{11}{4} \pi$
(B) $2(e-1) \pi$
(C) $\left(e-\frac{3}{2}\right) \pi$
(D) $\left(e-\frac{6}{5}\right) \pi$
▶️Answer/Explanation
Ans:D
Example 5
Let $R$ be the region between the graphs of $y=1+\sin (\pi x)$ and $y=x^3$ from $x=0$ to $x=1$. The volume of the solid obtained by revolving $R$ about the $x$-axis is given by
(A) $\pi \int_0^1\left[1+\sin (\pi x)-x^3\right] d x$
(B) $\pi \int_0^1\left[(1+\sin (\pi x))^2-x^6\right] d x$
(C) $\pi \int_0^1\left[1+\sin (\pi x)-x^3\right]^2 d x$
(D) $2 \pi \int_0^1\left[1+\sin (\pi x)-x^3\right] d x$
▶️Answer/Explanation
Ans:B
Example 6
- Find the volume of the solid formed by revolving the region bounded by the graphs of $y=x^{1 / 3}, y=x^2$,
(a) about the $x$-axis
(b) about the $y$-axis.
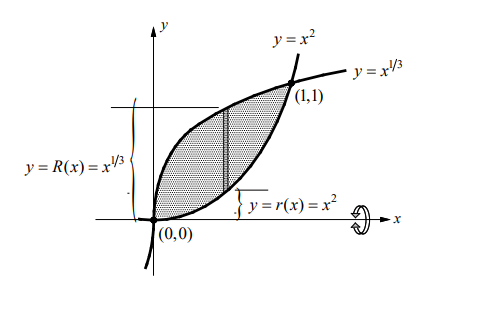
▶️Answer/Explanation
Solution
Sketch the graphs.
(a) The region runs from $x=0$ to $x=1$.
The volume is
$
\begin{aligned}
V & =\pi \int_a^b\left([R(x)]^2-[r(x)]^2\right) d x \\
& =\pi \int_0^1\left(\left[x^{1 / 3}\right]^2-\left[x^2\right]^2\right) d x \\
& =\pi \int_0^1\left(x^{2 / 3}-x^4\right) d x \\
& =\pi\left[\frac{3}{5} x^{5 / 3}-\frac{1}{5} x^5\right]_0^1 \quad y= \\
& =\frac{2 \pi}{5}
\end{aligned}
$
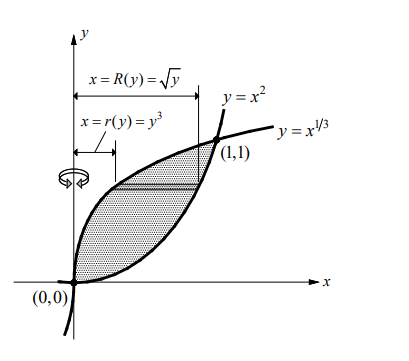
(b) The region runs from $y=0$ to $y=1$.
$
\begin{aligned}
V & =\pi \int_c^d\left([R(y)]^2-[r(y)]^2\right) d y \\
& =\pi \int_0^1\left([\sqrt{y}]^2-\left[y^3\right]^2\right) d y \\
& =\pi \int_0^1\left(y-y^6\right) d x \\
& =\pi\left[\frac{1}{2} y^2-\frac{1}{7} y^7\right]_0^1 \\
& =\frac{5 \pi}{14}
\end{aligned}
$
