Question
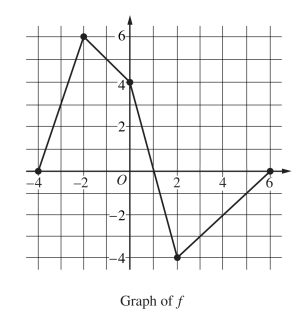
Let f be a continuous function defined on the closed interval −4 ≤ x ≤ 6. The graph of f , consisting of four line segments, is shown above. Let G be the function defined by \(G(x)=\int_{0}^{x}f(t)dt.\)
(a) On what open intervals is the graph of G concave up? Give a reason for your answer.
(b) Let P be the function defined by P (x) = G (x)• f(x). Find P'(3 ).
(c) Find \(\lim_{x\rightarrow 2}\frac{G(x)}{x^{2}-2x}.\)
(d) Find the average rate of change of G on the interval [−4, 2]. Does the Mean Value Theorem guarantee a value c, −4 < c < 2, for which G'(c) is equal to this average rate of change? Justify your answer.
▶️Answer/Explanation
Ans:
(a)
G'(x) = f(x)
G”(x) = f'(x)
On (-4, -2) and (2, 6), G(x) is concave up because f(x) (which is equal to G'(x)) has a positive slope / is increasing.
(b)
p'(x) = G'(x) f(x) + f'(x) G(x)
p'(3) = G'(3) f(3) + f'(3) G(3)
G'(x) = f(x) \(G(3)=\int_{0}^{3}f(t)dt=-\frac{7}{2}\)
\(p'(3)=(-3)(-3)+(1)\left (- \frac{7}{2} \right )\)
(c)
\(\lim_{x\rightarrow 2}G(x)=\lim_{x\rightarrow 2}(x^{2}-2x)=0\) Must be I’hopital’s rule
\(\int_{0}^{2}f(t)dt=0\)
\(\lim_{x\rightarrow 2}\frac{G'(x)}{2x-2}=\frac{f(2)}{4-2}=\frac{-4}{2}\)
(d)
\(\int_{0}^{2}f(t)dt\) \(\int_{0}^{-4}f(t)dt= -(3+9+3+1)\)
= -16
AROC of \(G = \frac{G(2)-G(-4)}{2-(-4)}=\frac{0-(16)}{2+4}=\frac{16}{6}=\frac{8}{3}\)
The meanvalue theorem does guarantee a value of -4<c<2, for which G'(c) is equal to average rate of chang. This is because G'(x) = f(t) and x = t exists for all values, -4<x=+t<2, meaning that G(x) is continuous on the closed interval and differentiable on the open interval.
Question
| t (years) | 2 | 3 | 5 | 7 | 10 |
| H(t) (meters) | 1.5 | 2 | 6 | 11 | 15 |
The height of a tree at time t is given by a twice-differentiable function H, where H (t) is measured in meters and t is measured in years. Selected values of H (t) are given in the table above.
(a) Use the data in the table to estimate H'(6 ). Using correct units, interpret the meaning of H'(6 ) in the context of the problem.
(b) Explain why there must be at least one time t, for 2 < t< 10 , such that H'(t) = 2.
(c) Use a trapezoidal sum with the four subintervals indicated by the data in the table to approximate the average height of the tree over the time interval 2 ≤ t ≤ 10.
(d) The height of the tree, in meters, can also be modeled by the function G, given by \(G(x)=\frac{100x}{1+x},\) where x is the diameter of the base of the tree, in meters. When the tree is 50 meters tall, the diameter of the base of the tree is increasing at a rate of 0.03 meter per year. According to this model, what is the rate of change of the height of the tree with respect to time, in meters per year, at the time when the tree is 50 meters tall?
▶️Answer/Explanation
Ans:
(a) \(H'(6)\approx \frac{H(7)-H(5)}{7-5}=\frac{11-6}{2}=\frac{5}{2}\)
H′(6) is the rate at which the height of the tree is changing, in meters per year, at time t = 6 years.
(b) \(\frac{H(5)-H(3)}{5-3}=\frac{6-2}{2}=2\)
Because H is differentiable on 3 ≤ t ≤ 5, H is continuous on 3 ≤ t ≤ 5.By the Mean Value Theorem, there exists a value c, 3 < c < 5, such that H ‘(c) = 2.
(c) The average height of the tree over the time interval 2 ≤ t ≤ 10 is given by \(\frac{1}{10-2}\int_{2}^{10}H(t)dt.\)
\(\frac{1}{8}\int_{2}^{10}H(t)dt\approx \frac{1}{8}\left ( \frac{1.5+2}{2}\cdot 1+\frac{2+6}{2}\cdot 2+\frac{6+11}{2}\cdot 2+\frac{11+15}{2}\cdot 3 \right )\)
\(=\frac{1}{8}(65.75)=\frac{263}{32}\)
The average height of the tree over the time interval 2 ≤ t ≤ 10 is \(\frac{263}{32}\) meters.
(d) G(x) = 50 ⇒ x = 1
\(\frac{d}{dt}(G(x))=\frac{d}{dx}(G(x))\cdot \frac{dx}{dt}=\frac{(1+x)100-100x\cdot 1}{(1+x)^{2}}\cdot \frac{dx}{dt}=\frac{100}{(1+x)^{2}}\cdot \frac{dx}{dt}\)
\(\frac{d}{dt}(G(x))|_{x=1}=\frac{100}{(1+1)^{2}}\cdot 0.03=\frac{3}{4}\)
According to the model, the rate of change of the height of the tree with respect to time when the tree is 50 meters tall is \(\frac{3}{4}\) meter per year.
Question:
Let f be the function defined by f(x) = cos (2 x) + esin x .
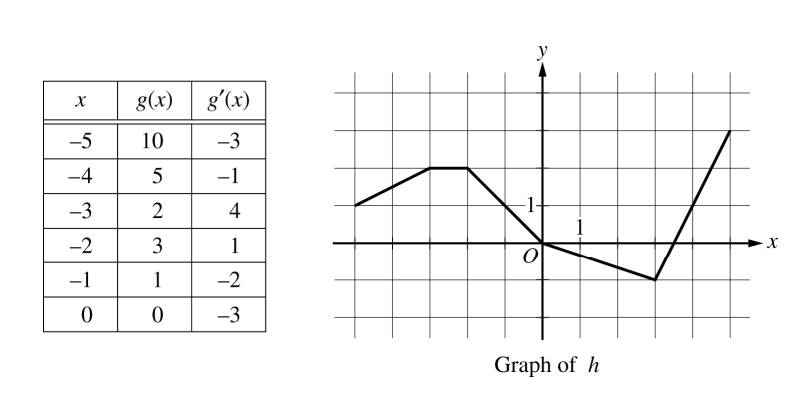
Let g be a differentiable function. The table above gives values of g and its derivative g’ at selected values of x.
Let h be the function whose graph, consisting of five line segments, is shown in the figure above.
(a) Find the slope of the line tangent to the graph of f at x = π.
(b) Let k be the function defined by k(x) = h(f(x)). Find k'(π).
(c) Let m be the function defined by m(x) = g(-2x)•h(x). Find m'(2).
(d) Is there a number c in the closed interval [−5, -3 ] such that g'(c) = −4 ? Justify your answer.
▶️Answer/Explanation
Ans:
(a)
\({f}'(x) = -2sin (2x) + e^{sinx} (cos x)\)
\({f}'(π) = -2 sin (2π) + e^{sinx}(cos π)\)
\(= 0 + 1(-1)\)
\(= -1\)

(b)
\({k}'(x) = {h}'(f(x)) ({f}'(x))\)
\({k}'(π) = {h}'(f(π)){ f}'(π)\)
\(= {h}'(2) (-1)\)
\(= 1/3\)
cos (2π) + esinπ
\(1 + 1\)
(c)
In'(x) = [g'(-2x) (-2) •h(x)] + [h'(x)•g(-2x)]
In'(2) = [-2g'(-4)•h(2)] + [h'(2)•g(-4)]
=(2•-2/3) + (-1/3 •5)
\(= -4/3 + -5/3\)
\(= -9/3\)
\(= -3\)
(d)
g(x) = differentiable →g(x) continuous is mean value theorem states that
\({f}'(c)=\frac{f(b)-f(a)}{b-a}\)
\(=\frac{g(-3)-g(-5)}{-3+5}=\frac{2-10}{2}\)
\(= -8/2\)
\(= -4\)
Yes, there’s aa number C is the closed interval such that \({g}'(c) = -4\)
Question:
Functions f, g, and h are twice-differentiable functions with g(2) = h(2) = 4. The line \(y = 4+\frac{2}{3}(x-2)\) is tangent to both the graph of g at x = 2 and the graph of h at x = 2.
(a) Find h'(2).
(b) Let a be the function given by a(x) = 3x3h(x). Write an expression for a'(x). Find a'(2).
(c) The function h satisfies \(h(x)=\frac{x^{2}-4}{1-(f(x))^{3}}\) for x ≠ 2. It is known that \(\lim_{x\rightarrow 2}h(x)\) can be evaluated using L’Hospital’s Rule. Use \(\lim_{x\rightarrow 2}h(x)\) to find f(2) and f'(2 ). Show the work that leads to your answers.
(d) It is known that g(x) ≤ h(x) for 1 < x < 3. Let k be a function satisfying g(x) ≤ k(x) ≤ h(x) for 1 < x < 3. Is k continuous at x = 2 ? Justify your answer.
▶️Answer/Explanation
Ans:
(a)
\(y = \frac{2}{3}(x-2)+4\)
point (2, 4) slope 2/3
h'(2) = 2/3
(b)
a'(x) = h'(x).3x3 + 9x2 h(x)
a'(2) = h'(2) . 3(2)3 + 9(2)2 h(2)
\(a'(2)=\frac{2}{3}\cdot 3\cdot 2^{3}+9\cdot 2^{2}\cdot 4\)
(c)
\(\lim_{x\rightarrow 2}\frac{x^{2}-4}{1-(f(x))^{3}}= \lim_{x\rightarrow 2}\frac{2x}{-3(f(x))^{2}.f'(x)}\) h (2) = 4
\(\therefore \lim_{x\rightarrow 2} h(x)\) must equal 4
\(\therefore \lim_{x\rightarrow 2} x^{2}-4=0\)
\( \lim_{x\rightarrow 2} 1-(f(x))^{3}=0\) if f(2) = 1 \(=\frac{2(2)}{-3(1)^{2}\cdot f'(2)}\)
∴ Indeterminate form 0/0 \(=\frac{4}{-3\cdot f'(2)}\) f'(2) must equal -1/3 so that \(\lim_{x\rightarrow 2} h(x) = 4\)
and L’Hopital’s rule applies \(=\frac{4}{-3\cdot -1/3}\)
Such that f(2) = 1 = 4/1
\(\lim_{x\rightarrow 2} h(x) = 4\) such that f(2) = 1 and f'(2) = -1/3
(d)
2 and h given as twice – differentiable ∴ g and h are continuous for 1 < x < 3
g(x) ≤ k(x) ≤ h(x)
\(\lim_{x\rightarrow 2} g(x) = 4\) because g continuous and g(2) = 4
\(\lim_{x\rightarrow 2} h(x) = 4\) because h continuous and h(2) = 4
By squeeze theorem, \(\lim_{x\rightarrow 2} k(x) = 4\)
k is between or equal to g and h for 1 < x < 3, given g(2) = 4 h (2) , meaning k(2) must equal 4, and \(\lim_{x\rightarrow 2} k(x) = 4\) so k(x) is continuous at x = 2
Question:
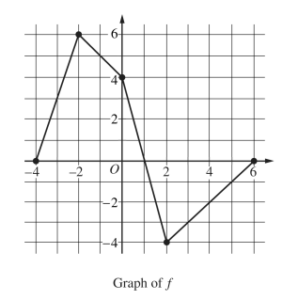
Let f be a continuous function defined on the closed interval −4 ≤ x ≤ 6. The graph of f , consisting of four line segments, is shown above. Let G be the function defined by \(G(x)=\int_{0}^{x}f(t)dt.\)
(a) On what open intervals is the graph of G concave up? Give a reason for your answer.
(b) Let P be the function defined by P (x) = G (x)• f(x). Find P'(3 ).
(c) Find \(\lim_{x\rightarrow 2}\frac{G(x)}{x^{2}-2x}.\)
(d) Find the average rate of change of G on the interval [−4, 2]. Does the Mean Value Theorem guarantee a value c, −4 < c < 2, for which G'(c) is equal to this average rate of change? Justify your answer.
▶️Answer/Explanation
Ans:
(a)
G'(x) = f(x)
G”(x) = f'(x)
On (-4, -2) and (2, 6), G(x) is concave up because f(x) (which is equal to G'(x)) has a positive slope / is increasing.
(b)
p'(x) = G'(x) f(x) + f'(x) G(x)
p'(3) = G'(3) f(3) + f'(3) G(3)
G'(x) = f(x) \(G(3)=\int_{0}^{3}f(t)dt=-\frac{7}{2}\)
\(p'(3)=(-3)(-3)+(1)\left (- \frac{7}{2} \right )\)
(c)
\(\lim_{x\rightarrow 2}G(x)=\lim_{x\rightarrow 2}(x^{2}-2x)=0\) Must be I’hopital’s rule
\(\int_{0}^{2}f(t)dt=0\)
\(\lim_{x\rightarrow 2}\frac{G'(x)}{2x-2}=\frac{f(2)}{4-2}=\frac{-4}{2}\)
(d)
\(\int_{0}^{2}f(t)dt\) \(\int_{0}^{-4}f(t)dt= -(3+9+3+1)\)
= -16
AROC of \(G = \frac{G(2)-G(-4)}{2-(-4)}=\frac{0-(16)}{2+4}=\frac{16}{6}=\frac{8}{3}\)
The meanvalue theorem does guarantee a value of -4<c<2, for which G'(c) is equal to average rate of chang. This is because G'(x) = f(t) and x = t exists for all values, -4<x=+t<2, meaning that G(x) is continuous on the closed interval and differentiable on the open interval.