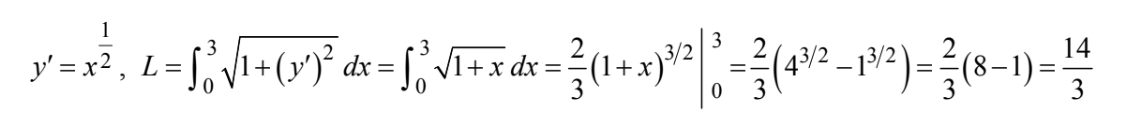Question
The length of the curve \(y = sin x\) from \(x = 0\) to \(x = 3π/4\) is given by
A \(\int_{0}^{3\pi /4}sinxdx\)
B \(\int_{0}^{3\pi /4}\sqrt{1+sin^2x}dx\)
C \(\int_{0}^{3\pi /4}\sqrt{1−cos^2x}dx\)
D \(\int_{0}^{3\pi /4}\sqrt{1+cos^2x}dx\)
Answer/Explanation
Question
Which of the following integrals gives the length of the graph of y =tan x between x = a and x=b,where \(0<a<b<\frac{\pi }{2}\)?
(A)\(\int_{a}^{b}\sqrt{x^{2}+tan^{2}}dx\)
(B)\(\int_{a}^{b}\sqrt{x+tanx}dx\)
(C)\(\int_{a}^{b}\sqrt{1+sec^{2}x}dx\)
(D)\(\int_{a}^{b}\sqrt{1+tan^{2}x}dx\)
(E)\(\int_{a}^{b}\sqrt{1+sec^{4}x}dx\)
Answer/Explanation
Ans:D
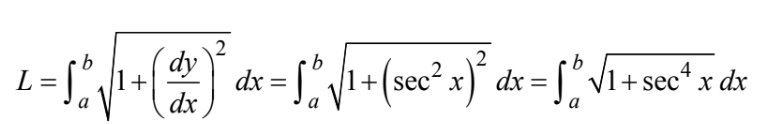
Question
The length of the curve ln sec y x = from x = 0 to x = b, where \(0<b<\frac{\pi }{2}\), may be expressed by which of the following integrals?
(A)\(\int_{0}^{b}secxdx\)
(B)\(\int_{0}^{b}sec^{2}dx\)
(C)\(\int_{0}^{b}(secxtanx)dx\)
(D)\((A)\int_{0}^{b}\sqrt{1+(Insec)^{2}}dx\)
(E\(\int_{0}^{b}\sqrt{1+\left ( sec^{2}xtan^{2}x \right )}\)
Answer/Explanation
Ans:A
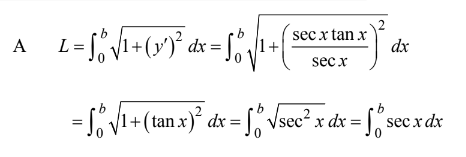
Question
What is the length of the arc of \( y=\frac{2}{3}x^{\frac{3}{2}}\) from x = 0 to x = 3?
(A)\(\frac{8}{3}\) (B) 4 (C) \(\frac{14}{3}\) (D)\( \frac{16}{3}\) (E) 7
Answer/Explanation
Ans:C