Question
Let f be a function with f(0) = 1 , f'(0) = 2 , and f”(0) = −2 . Which of the following could be the graph of the second-degree Taylor polynomial for f about x= 0 ?
A 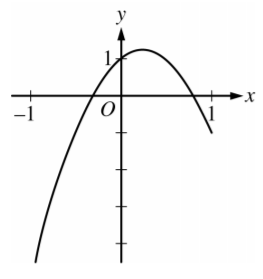
B 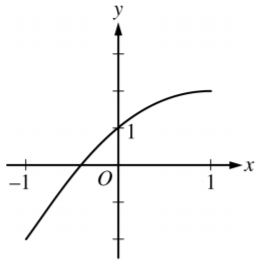
C 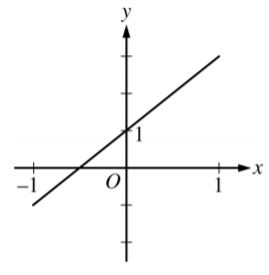
D 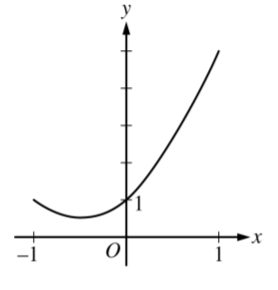
Answer/Explanation
Question
If a function f is continuous for all x and if f has a relative maximum at ( 1,4) − and a relative minimum at (3, 2) − , which of the following statements must be true?
(A) The graph of f has a point of inflection somewhere between x = −1 and x = 3.
(B) f ′ (- 1) = 0
(C) The graph of f has a horizontal asymptote.
(D) The graph of f has a horizontal tangent line at x = 3.
(E) The graph of f intersects both axes.
Answer/Explanation
Question
If a function f is continuous for all x and if f has a relative maximum at ( 1,4) − and a relative minimum at (3, 2) − , which of the following statements must be true?
(A) The graph of f has a point of inflection somewhere between x = −1 and x = 3.
(B) f ′ (- 1) = 0
(C) The graph of f has a horizontal asymptote.
(D) The graph of f has a horizontal tangent line at x = 3.
(E) The graph of f intersects both axes.
Answer/Explanation
Ans:D
Substitute −x for x in 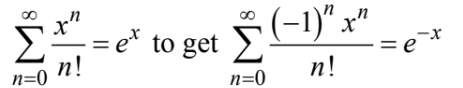
Question
The coefficient of \(x^6\) in the Taylor series expansion about x = 0 for \(f(x)=sin\left ( x^{2} \right )\) is
(A) \(-\frac{1}{6}\) (B) 0 (C) \(\frac{1}{120}\) (D) \(\frac{1}{6}\) (E) 1
Answer/Explanation
Ans:A
