Question
Let y = f(x) be the solution to the differential equation \(\frac{dy}{dx}={f}’ (x)\) with initial condition f(1) = 5 . Selected values of f ‘(x) are given in the table above. What is the approximation for f(2) if Euler’s method is used with a step size of 0.5, starting at x= 1 ?
A \(5.35\)
B \(5.45\)
C \(5.50\)
D \(5.90\)
Answer/Explanation
Question
The approximate value of\( y= \sqrt{4+sinx}\) at x=0.12, obtained from the tangent to the graph at x = 0, is
(A) 2.00 (B) 2.03 (C) 2.06 (D) 2.12 (E) 2.24
Answer/Explanation
Ans:B
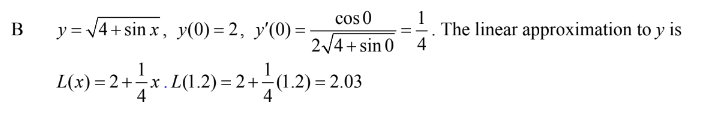
Question
Given \(\frac{\mathrm{d} y}{\mathrm{d} t}=2\sin (4\pi t)\) and y(1) = 2, approximate y(3) using five steps.
(A) 8
(B) -2
(C) 17
(D) 2
Answer/Explanation
Ans:(D)
The problem requires us to use Euler’s method. First, calculate the step size.
\(\Delta t=\frac{3-1}{5}=0.4\)
Recall that the general equation for calculating approximations with Euler’s method is
\(y_{n}=y_{n-1}+\Delta x.f'(x_{n-1},y_{n-1})\)
Now construct a table to insert the approximations at each step.

Question
Use Euler’s method and a step size of \(\Delta x=0.2\) to compute y(1) if y(x) is the solution of the differential equation \(\frac{\mathrm{d} y}{\mathrm{d} x}+4x^{3}y=2x^{3}\) with initial condition y(0) = 2.
(A) 4.8
(B) 1.19
(C) -12.45
(D) 5.67
Answer/Explanation
Ans:(B)
Recall that the general equation for calculating approximations with Euler’s method is
\(y_{n}=y_{n-1}+\Delta x.f'(x_{n-1},y_{n-1})\)
For the case of the the evaluation, transform \(\frac{\mathrm{d} y}{\mathrm{d} x}+4x^{3}y=2x^{3}\) to \(\frac{\mathrm{d} y}{\mathrm{d} x}=2x^{3}(1-2y)\)
Now construct a table to insert the approximations at each step.

