Question
Let y = f(x) be the particular solution to the differential equation \(\frac{dy}{dx}=y\cdot (x In x)\) with initial condition f(1) = 4 . It can be shown that f”(1) = 4.
(a) Write the second-degree Taylor polynomial for f about x = 1. Use the Taylor polynomial to approximate f(2) .
(b) Use Euler’s method, starting at x = 1 with two steps of equal size, to approximate f(2) . Show the work that leads to your answer.
(c) Find the particular solution y = f(x) to the differential equation \(\frac{dy}{dx}=y\cdot (x In x)\) with initial condition f(1) = 4 .
Answer/Explanation
Ans:
(a)
\(\frac{dy}{dx}= 4.1 In 1\)
\(P_{2}(x)=4+In 1 (x-1)+\frac{4(x-1)^{2}}{2!}\) \(P_{2}(x)=4+\frac{4(x-1)^{2}}{2!}\)
\(P_{2}(2)=4+\frac{4(2-1)^{2}}{2!}= 4+2 = 6\)
(b)
\(\frac{dy}{dx}= 4\cdot 1.5 In 1.5\)
6 In 1.5
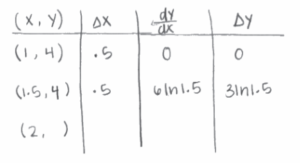
f(2) = 4 + 3 In 1.5
(c)
\(\frac{dy}{dx}= y\cdot sin x\)
\(\frac{1}{y}dy= x In x dx\) u = In x dv = x dx
\(\int \frac{1}{y}dy= \int x In x dx\) \(du = \frac{1}{x}dx\) \(v = \frac{1}{x}x^{2}\)
\(In y = \frac{1}{2}x^{2}In x -\frac{1}{4}x^{2}+ c\)
\(In 4 = \frac{1}{2}In 1 -\frac{1}{4}+ c\)
\(In 4 + \frac{1}{4}= c\)
\(In y =\frac{1}{2}x^{2}In x- \frac{1}{4}x^{2}+In 4 + \frac{1}{4}\)
\(y =4e^{\frac{1}{2}x^{2}In x}- \frac{1}{4}x^{2} + \frac{1}{4}\)
Question
Consider the differential equation \(\frac{dy}{dx}=\frac{y^{2}}{x-1}.\)
(a) On the axes provided, sketch a slope field for the given differential equation at the six points indicated.
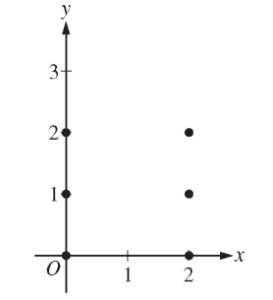
(b) Let y = f(x) be the particular solution to the given differential equation with the initial condition f(x) = 3. Write an equation for the line tangent to the graph of y=f(x) at x= 2.
Use your equation to approximate f(2.1).
(c) Find the particular solution y = f (x) to the given differential equation with the initial condition f (2) = 3.
Answer/Explanation
Ans:
(a) 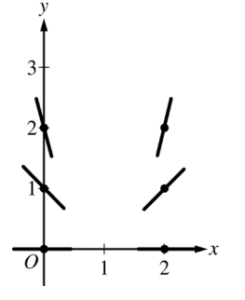
(b) \(\frac{dy}{dx}_{(x,y)=(2,3)}=\frac{3^{2}}{2-1}=9\)
An equation for the tangent line is y = 9(x – 2) + 3.
f(2.1) ≈ 9(2.1-2) + 3 = 3.9
(c) \(\frac{1}{y^{2}}dy=\frac{1}{x-1}dx\)
\(\int \frac{1}{y^{2}}dy=\int \frac{1}{x-1}dx\)
\(-\frac{1}{y}= In|x-1|+C\)
\(-\frac{1}{3}= In|2-1|+C\Rightarrow C=-\frac{1}{3}\)
\(-\frac{1}{y}= In|x-1|-\frac{1}{3}\)
\(y= \frac{1}{\frac{1}{3}-In(x-1)}\)
Note: This solution is valid for 1 < x < 1 + e1/3.
Question
Consider the differential equation \(\frac{dy}{dx}=2x – y.\)
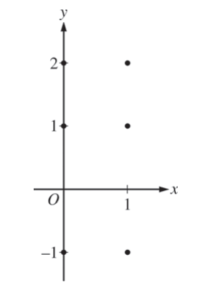
(a) On the axes provided, sketch a slope field for the given differential equation at the six points indicated.
(b) Find \(\frac{d^{2}y}{dx^{2}}\) in terms of x and y. Determine the concavity of all solution curves for the given differential equation in Quadrant II. Give a reason for your answer.
(c) Let y = f(x) be the particular solution to the differential equation with the initial condition f(2) = 3. Does f have a relative minimum, a relative maximum, or neither at x =2 ? Justify your answer.
(d) Find the values of the constants m and b for which y = mx + b is a solution to the differential equation.
Answer/Explanation
Ans:
(a) Slopes where x = 0
slopes where x = 1
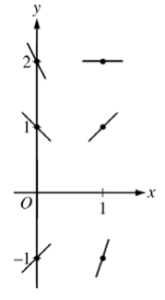
(b) \(\frac{d^{2}y}{dx^{2}}= 2 – \frac{dy}{dx}= 2 -(2x-y)=2-2x+y\)
In Quadrant II, x < 0 and y > 0, so 2 – 2x + y > 0. Therefore, all solution curves are concave up in Quadrant II.
(c) \(\frac{dy}{dx}|_{(x,y)=(2,3)}=2(2)-3 = 1\neq 0\)
Therefore, f has neither a relative minimum nor a relative maximum at x = 2.
(d) \(y = mx + b \Rightarrow \frac{dy}{dx}=\frac{d}{dx}(mx + b)=m\)
2x – y = m
2x – (mx + b) = m
(2 – m)x – (m + b) = 0
2 – m = 0 ⇒ m = 2
b = -m ⇒ b = -2
Therefore, m = 2 and b = -2.
Question
Consider the differential equation \(\frac{dy}{dx}=y^{2}(2x+2).\) Let y = f(x) be the particular solution to the differential equation with initial condition f (0)= -1.
(a) Find \(\lim_{x\rightarrow 0}\frac{f(x)+1}{sinx}.\) Show the work that leads to your answer.
(b) Use Euler’s method, starting at x 0 with two steps of equal size, to approximate \(f\left ( \frac{1}{2} \right )\).
(c) Find y = f(x), the particular solution to the differential equation with initial condition f(0) = – 1.
Answer/Explanation
Ans:
(a) \(\lim_{x\rightarrow 0}(f(x)+1)=-1+1=0 and \lim_{x\rightarrow 0} sin x = 0\)
Using L’Hospital’s Rule,
\(\lim_{x\rightarrow 0}\frac{f(x)+1}{sinx}=\lim_{x\rightarrow 0} \frac{f'(x)}{cos x}=\frac{f'(0)}{cos 0}=\frac{(-1)^{2}\cdot 2}{1}=2\)
(b) \(f\left ( \frac{1}{4} \right )\approx f(0)+f'(0)\left ( \frac{1}{4} \right )\)
\(=-1+(2)\left ( \frac{1}{4} \right )=-\frac{1}{2}\)
\(f\left ( \frac{1}{2} \right )\approx f\left ( \frac{1}{4} \right )+f’\left ( \frac{1}{4} \right )\left ( \frac{1}{4} \right )\)
\(=-\frac{1}{2}+\left ( -\frac{1}{2} \right )^{2}\left ( 2\cdot \frac{1}{4}+2 \right )\left ( \frac{1}{4} \right )=-\frac{11}{32}\)
(c) \(\frac{dy}{dx}=y^{2}(2x+2)\)
\(\frac{dy}{y^{2}}=(2x+2)dx\)
\(\int \frac{dy}{y^{2}}=\int (2x+2)dx\)
\(-\frac{1}{y}=x^{2}+2x+C\)
\(-\frac{1}{-1}=0^{2}+2\cdot 0+C\Rightarrow C = 1\)
\(-\frac{1}{y}=x^{2}+2x+ 1\)
\(y=-\frac{1}{x^{2}+2x+ 1}=-\frac{1}{(x+1)^{2}}\)
Note: This solution is valid for x > -1.
Question
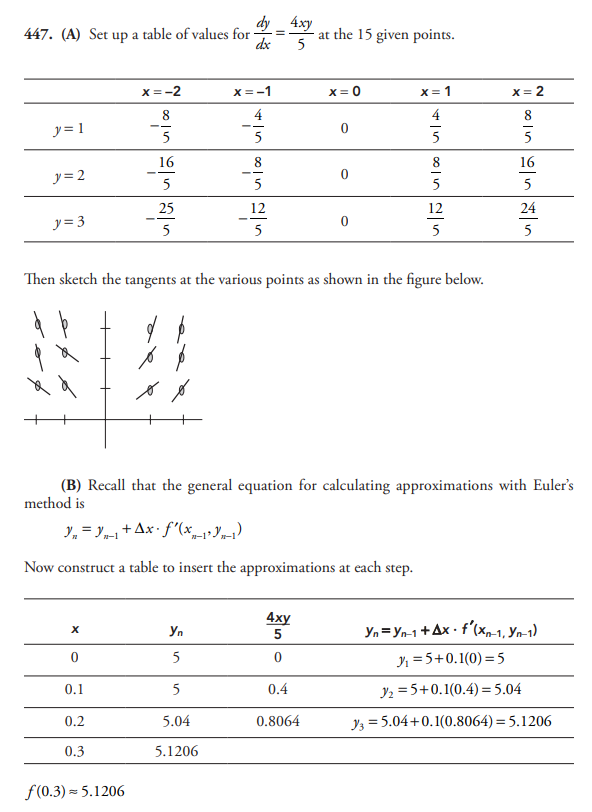
Consider the differential equation given by \(dy/dx=\frac{4xy}{5}\) .
(A) On the axis provided below, sketch a slope field for the given differential equation at the points indicated.
(B) Let y = f (x) be the particular solution to the given differential equation with initial condition f (0) = 5. Use Euler’s method and a step size of 0.1 to approximate f (0.3). Show the work that leads to your answer.
(C) Find the particular solution y = f (x) to the given differential equation with initial condition f (0) = 5.
(D) Use your solution above to find f (0.3).
Answer/Explanation

Question
At the beginning of 2010, a landfill contained 1400 tons of solid waste. The increasing function W models the total amount of solid waste stored at the landfill. Planners estimate that W will satisfy the differential equation \( \frac{dW}{dt}=\frac{1}{25}(W-300) \) for the next 20 years. W is measured in tons, and t is measured in years from the start of 2010.
(a) Use the line tangent to the graph of W at t = 0 to approximate the amount of solid waste that the landfill contains at the end of the first 3 months of 2010 \( (time ~t = \frac{1}{4}) \)
(b) Find \(\frac{d^{2}W}{dt^{2}}\) in terms of W. Use \(\frac{d^{2}W}{dt^{2}}\) to determine whether your answer in part (a) is an underestimate or an overestimate of the amount of solid waste that the landfill contains at time \( t = \frac{1}{4}. \)
(c) Find the particular solution W = W(t) to the differential equation \(\frac{dW}{dt}=\frac{1}{25}(W-300)\) with initial condition W(0) =1400.
Answer/Explanation
Ans:
(a)
at t = 0, w = 1400
so
\(\frac{dW}{dt}|_{t=0}=\frac{1}{25}(1100)=44 tons/year = W'(0)\)
W(x+a) ≈ W(x) + aW'(x)
\(W(0+\frac{1}{4})\approx W(0)+\frac{1}{4}W'(0)\)
\(W(\frac{1}{4})\approx 1400+11\)
\(W(\frac{1}{4})\approx 1411 tons\)
There will be about 1411 tons of landfill after 3 months.
(b)
\(\frac{dW}{dt}=\frac{1}{25}W-12\) So \(\frac{d^{2}W}{dt^{2}}\) is always positive b/c W > 300.
\(\frac{d^{2}W}{dt^{2}}=\frac{1}{25}\frac{dW}{dt}\)
\(\frac{d^{2}W}{dt}=\frac{1}{625}(W-300)\)
The answer in part a is an underestimate because since \(\frac{d^{2}W}{dt^{2}}\) is always positive for t > 0, the graph of w is concave up, so the linearization of w is an underestimate.
(c)
\( \frac{dW}{dt}=\frac{1}{25}(W-300)\)
\(\int \frac{dW}{W-300}=\int \frac{1}{25}dt\)
\(e^{\xi n|W-300|}=e^{\frac{1}{25}t+c}\)
can remove abs value b/c w > 300. (iner fn)
\(|W-300|=Ce^{\frac{1}{25}t}\)
Initial condition W(0) = 1400
1400 – 300 = C e0
1100 = c
\(W-300=1100e^{\frac{1}{25}t}\)
\(W= W(t)=1100e^{\frac{1}{25}t}+300\)
