Question
Let g be a twice-differentiable, increasing function of t. If g(0) = 20 and g(10) = 220, which of the following must be true on the interval 0 < t < 10?
A g'(t) = 0 for some t in the interval.
B g'(t) = 20 for some t in the interval.
C g”(t) = 0 for some t in the interval.
D g”(t) > 0 for all t in the interval.
Answer/Explanation
Question
The Mean Value Theorem guarantees the existence of a special point on the graph of \(Y=\sqrt{x} \)between (0,0 ) and (4,2 ) . What are the coordinates of this point?
(A) (2,1)
(B) (1,1)
(C)\(\left ( 2,\sqrt{2} \right )\)
(D)\(\left ( \frac{1}{2},\frac{1}{\sqrt{2}} \right )\)
(E) None of the above
Answer/Explanation
Question
If c is the number that satisfies the conclusion of the Mean Value Theorem for \(f(x)=x^{3}-2x^{2}\) on the interval 0 ≤ 2, ≤x then c =
(A) 0 (B) \(\frac{1}{2}\) (C) 1 (D) \(\frac{4}{3}\) (E) 2
Answer/Explanation
Ans:D
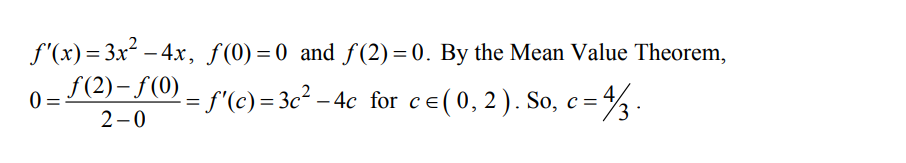
Question
The function f(x) is differentiable on the interval (1, 5), except at a nonremovable point of discontinuity at x = 3 with f ′(1) = -2 and f ′(5) = 2.
(A) The Mean Value Theorem for Derivatives says there must be a point at x = c, with 1 < c < 5, where f ′(c) = 0.
(B) The Intermediate Value Theorem for Derivatives says there must be a point at x = c, with 1 < c < 5, where f ′(c) = 1.
(C) The Intermediate Value Theorem for Derivatives says there must not be a point at x = c, with 1 < c < 5, where f ′(c) = 0.
(D) Neither the Mean Value Theorem for Derivatives nor the Intermediate Value Theorem for Derivatives apply here.
Answer/Explanation
Ans:(D)
