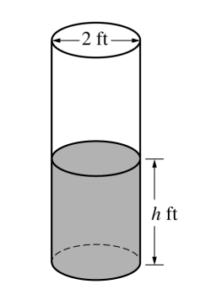
Question
A cylindrical barrel with a diameter of 2 feet contains collected rainwater, as shown in the figure above. The water drains out through a valve (not shown) at the bottom of the barrel. The rate of change of the height h of the water in the barrel with respect to time t is modeled by \(\frac{dh}{dt}=-\frac{1}{10}\sqrt{h},\) where h is measured in feet and
t is measured in seconds. (The volume V of a cylinder with radius r and height h is V = πr2h.)
(a) Find the rate of change of the volume of water in the barrel with respect to time when the height of the water is 4 feet. Indicate units of measure.
(b) When the height of the water is 3 feet, is the rate of change of the height of the water with respect to time increasing or decreasing? Explain your reasoning.
(c) At time t = 0 seconds, the height of the water is 5 feet. Use separation of variables to find an expression for h in terms of t.
Answer/Explanation
Ans:
(a) \(V = \pi r^{2}h=\pi (1)^{2}h=\pi h\)
\(\frac{dV}{dt}|_{h=4}=\pi \frac{dh}{dt}|_{h=4}=\pi \left ( -\frac{1}{10}\sqrt{4} \right )=-\frac{\pi }{5}\) cubic feet per second
(b) \(\frac{d^{2}h}{dt^{2}}=-\frac{1}{20\sqrt{h}}\cdot \frac{dh}{dt}=-\frac{1}{20\sqrt{h}}\cdot \left ( -\frac{1}{10} \sqrt{h}\right )=\frac{1}{200}\)
Because \(\frac{d^{2}h}{dt^{2}}=\frac{1}{200}>0\) for h > 0, the rate of change of the height is increasing when the height of the water is 3 feet.
(c) \(\frac{dh}{\sqrt{h}}=-\frac{1}{10}dt\)
\(\int \frac{dh}{\sqrt{h}}=\int -\frac{1}{10}dt\)
\(2\sqrt{h}=-\frac{1}{10}t+C\)
\(2\sqrt{5}=-\frac{1}{10}\cdot 0+C\Rightarrow C = 2\sqrt{5}\)
\(2\sqrt{h}=-\frac{1}{10}t+2\sqrt{5}\)
\(h(t)=\left ( -\frac{1}{20}t+\sqrt{5} \right )^{2}\)
Question
| h (feet) | 0 | 2 | 5 | 10 |
| A(h) (square feet) | 50.3 | 14.4 | 6.5 | 2.9 |
A tank has a height of 10 feet. The area of the horizontal cross section of the tank at height h feet is given by the function A, where A (h) is measured in square feet. The function A is continuous and decreases as h increases. Selected values for A (h) are given in the table above.
(a) Use a left Riemann sum with the three subintervals indicated by the data in the table to approximate the volume of the tank. Indicate units of measure.
(b) Does the approximation in part (a) overestimate or underestimate the volume of the tank? Explain your reasoning.
(c) The area, in square feet, of the horizontal cross section at height h feet is modeled by the function f given by \(f(h)=\frac{50.3}{e^{0.2h}+h}\) Based on this model, find the volume of the tank. Indicate units of measure.
(d) Water is pumped into the tank. When the height of the water is 5 feet, the height is increasing at the rate of 0.26 foot per minute. Using the model from part (c), find the rate at which the volume of water is changing with respect to time when the height of the water is 5 feet. Indicate units of measure.
Answer/Explanation
Ans:
(a) \(Volume = \int_{0}^{10}A(h)dh\)
≈ (2 – 0) · A(0) + (5 -2) · A(2) + (10 – 5) · A(5)
= 2 · 50.3 + 3.14.4 + 5 · 6.5
= 176.3 cubic feet
(b) The approximation in part (a) is an overestimate because a left Riemann sum is used and A is decreasing.
(c) \(\int_{0}^{10}f(h)dh=101.325338\)
The volume is 101.325 cubic feet.
(d) Using the model, \(V(h)=\int_{0}^{h}f(x)dx.\)
\(\frac{dV}{dt}|_{h=5}=\left [ \frac{dV}{dh}\cdot \frac{dh}{dt} \right ]_{h=5}\)
\(=\left [f(h)\cdot \frac{dh}{dt} \right ]_{h=5}\)
When h = 5, the volume of water is changing at a rate of 1.694 cubic feet per minute.
Question
| t (hours) | 0 | 1 | 3 | 6 | 8 |
| R(t) (liters / hour) | 1340 | 1190 | 950 | 740 | 700 |
Water is pumped into a tank at a rate modeled by \(W(t)=2000e^{-t^{2}/20}\) liters per hour for 0 ≤ t ≤ 8, where t is measured in hours. Water is removed from the tank at a rate modeled by R (t) liters per hour, where R is differentiable and decreasing on 0 ≤ t ≤ 8. Selected values of R(t) are shown in the table above. At time t = 0, there are 50,000 liters of water in the tank.
(a) Estimate R'(2). Show the work that leads to your answer. Indicate units of measure.
(b) Use a left Riemann sum with the four subintervals indicated by the table to estimate the total amount of water removed from the tank during the 8 hours. Is this an overestimate or an underestimate of the total amount of water removed? Give a reason for your answer.
(c) Use your answer from part (b) to find an estimate of the total amount of water in the tank, to the nearest liter, at the end of 8 hours.
(d) For 0 ≤ t ≤ 8, is there a time t when the rate at which water is pumped into the tank is the same as the rate at which water is removed from the tank? Explain why or why not.
Answer/Explanation
Ans:
(a) \(R'(2)\approx \frac{R(3)-R(1)}{3-1}=\frac{950-1190}{3-1}=-120 liters/hr^{2}\)
(b) The total amount of water removed is given by \(\int_{0}^{8}R(t)dt.\)
\(\int_{0}^{8}R(t)dt\approx 1\cdot R(0)+2\cdot R(1)+3\cdot R(3)+2\cdot R(6)\)
= 1(1340) + 2(1190) + 3(950) +2(740)
=8050 liters
This is an overestimate since R is a decreasing function.
(c)
\(Total \approx 50000+\int_{0}^{8}W(t)dt-8050\)
=50000 + 7836.195325 – 8050 ≈ 49786 liters
(d) W(0) – R(0) > 0, W(8) – R(8) < 0, and W(t) – R(t) is continuous.
Therefore, the Intermediate value Theorem guarantees at least one time t, 0 < t < 8, for which W(t) – R(t) = 0, or W(t) = R(t).
For this value of t, the rate at which water is pumped into the tank is the same as the rate at which water is removed from the tank.
Question
Consider the differential equation \(\frac{dy}{dx}=y^{2}(2x+2).\) Let y = f(x) be the particular solution to the differential equation with initial condition f (0)= -1.
(a) Find \(\lim_{x\rightarrow 0}\frac{f(x)+1}{sinx}.\) Show the work that leads to your answer.
(b) Use Euler’s method, starting at x 0 with two steps of equal size, to approximate \(f\left ( \frac{1}{2} \right )\).
(c) Find y = f(x), the particular solution to the differential equation with initial condition f(0) = – 1.
Answer/Explanation
Ans:
(a) \(\lim_{x\rightarrow 0}(f(x)+1)=-1+1=0 and \lim_{x\rightarrow 0} sin x = 0\)
Using L’Hospital’s Rule,
\(\lim_{x\rightarrow 0}\frac{f(x)+1}{sinx}=\lim_{x\rightarrow 0} \frac{f'(x)}{cos x}=\frac{f'(0)}{cos 0}=\frac{(-1)^{2}\cdot 2}{1}=2\)
(b) \(f\left ( \frac{1}{4} \right )\approx f(0)+f'(0)\left ( \frac{1}{4} \right )\)
\(=-1+(2)\left ( \frac{1}{4} \right )=-\frac{1}{2}\)
\(f\left ( \frac{1}{2} \right )\approx f\left ( \frac{1}{4} \right )+f’\left ( \frac{1}{4} \right )\left ( \frac{1}{4} \right )\)
\(=-\frac{1}{2}+\left ( -\frac{1}{2} \right )^{2}\left ( 2\cdot \frac{1}{4}+2 \right )\left ( \frac{1}{4} \right )=-\frac{11}{32}\)
(c) \(\frac{dy}{dx}=y^{2}(2x+2)\)
\(\frac{dy}{y^{2}}=(2x+2)dx\)
\(\int \frac{dy}{y^{2}}=\int (2x+2)dx\)
\(-\frac{1}{y}=x^{2}+2x+C\)
\(-\frac{1}{-1}=0^{2}+2\cdot 0+C\Rightarrow C = 1\)
\(-\frac{1}{y}=x^{2}+2x+ 1\)
\(y=-\frac{1}{x^{2}+2x+ 1}=-\frac{1}{(x+1)^{2}}\)
Note: This solution is valid for x > -1.
Question
On a certain workday, the rate, in tons per hour, at which unprocessed gravel arrives at a gravel processing plant is modeled by \(G(t)=90+45 cos\left ( \frac{t^{2}}{18} \right ),\) where t is measured in hours and 0 ≤ t ≤ 8. At the beginning of the workday (t = 0) , the plant has 500 tons of unprocessed gravel. During the hours of operation, 0 ≤ t ≤ 8, the plant processes gravel at a constant rate of 100 tons per hour.
(a) Find G'(5) . Using correct units, interpret your answer in the context of the problem.
(b) Find the total amount of unprocessed gravel that arrives at the plant during the hours of operation on this workday.
(c) Is the amount of unprocessed gravel at the plant increasing or decreasing at time t = 5 hours? Show the work that leads to your answer.
(d) What is the maximum amount of unprocessed gravel at the plant during the hours of operation on this workday? Justify your answer.
Answer/Explanation
Ans:
(a) G'(5) = -24.588 (or – 24.587)
The rate at which gravel is arriving is decreasing by 24.588 (or 24.587) tons per hour per hour at time t=5 hours.
(b) \(\int_{0}^{8}G(t)dt=825.551 tons\)
(c) G(5) = 98.140764 < 100
At time t = 5, the rate at which unprocessed gravel is arriving is less than the rate at which it is being processed. Therefore, the amount of unprocessed gravel at the plant is
decreasing at time t = 5.
(d) The amount of unprocessed gravel at time t is given by
\(A(t)=500+\int_{0}^{t}(G(s)-100)ds.\)
A'(t) = G(t) – 100 = 0 ⇒ t = 4.923480

The maximum amount of unprocessed gravel at the plant during this workday is 635.376 tons.
Question
A conical funnel has a base diameter of 6 cm and a height of 5 cm. The funnel sits over a cylindrical can with an open top. The can has a diameter of 4 cm and a height of 5 cm. The funnel is initially full, but water is draining from the funnel bottom into the can at a constant rate of \(2cm^{3}/s\). Answer the following questions. (Show your work.)
(A) How fast is the water level in the funnel falling when the water is 2.5 cm high?
(B) How fast is the water level in the can rising?
(C) Will the can overflow? If not, how high will the final level of water be in the can?
Answer/Explanation
(A)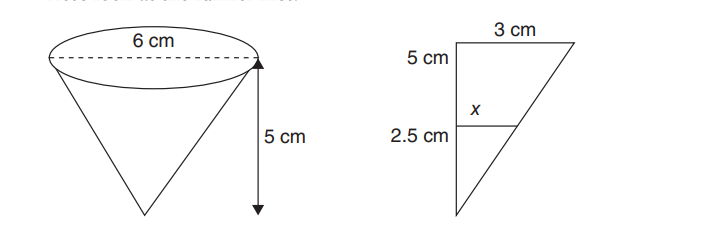
\(\frac{3}{5}=\frac{r}{h}\)
3h=5r
\(r=\frac{3h}{5}\)
\(V=\frac{1}{3}\pi r^{2}h\)
\(V=\frac{1}{3}\pi \left ( \frac{3h}{5} \right )^{2}h\)
\(V=\frac{1}{3}\pi \left ( \frac{9h^{2}}{25} \right )h\)
\(V=\frac{3}{25}\pi h^{3}\)
\(\frac{\mathrm{d} V}{\mathrm{d} t}=3\left ( \frac{3}{25} \right )\pi h^{2}\frac{\mathrm{d} h}{\mathrm{d} t}\)
\(\frac{\mathrm{d} V}{\mathrm{d} t}=\left ( \frac{9}{25} \right )\pi h^{2}\frac{\mathrm{d} h}{\mathrm{d} t}\)
\(\frac{\mathrm{d} V}{\mathrm{d} t}=-2cm^{3}/s\)
\(-2=\left ( \frac{9}{25} \right )\pi h^{2}\frac{\mathrm{d} h}{\mathrm{d} t}\)
\(\frac{\mathrm{d} h}{\mathrm{d} t}=-\frac{50}{9\pi h^{2}}\)
\(\frac{\mathrm{d} h}{\mathrm{d} t}=-\frac{50}{9\pi (2.5)^{2}}\)
\(\frac{\mathrm{d} h}{\mathrm{d} t}=-\frac{50}{9\pi \left ( \frac{25}{4} \right )}=-\frac{8}{9\pi }=0.28cm/s\)
(B) 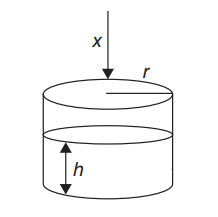
\(V=\pi r^{2}h\)
\(\frac{\mathrm{d} V}{\mathrm{d} t}=\pi r^{2}\frac{\mathrm{d} h}{\mathrm{d} t}\) (r is constant)
\(\pi r^{2}\frac{\mathrm{d} h}{\mathrm{d} t}=\frac{\mathrm{d} V}{\mathrm{d} t}\)
\(\frac{\mathrm{d} h}{\mathrm{d} t}=\frac{1}{\pi r^{2}}\left ( \frac{\mathrm{d} V}{\mathrm{d} t} \right )\)
\(\frac{\mathrm{d} h}{\mathrm{d} t}=\frac{1}{\pi (2cm)^{2}}(2cm^{3}/min)\)
\(\frac{\mathrm{d} h}{\mathrm{d} t}=\left ( \frac{1cm/s}{2\pi } \right )=0.16cm/s\)
(C) 
Question
You are to make a cylindrical tin can with closed top to hold \(360 cm^3\).
(A) Make a drawing and label what is given.
(B) What are its dimensions if the amount of tin used is to be the minimum?
(C) What is the surface area?
Answer/Explanation
(A) 
(B)\(V=\pi r^{2}h\)
\(360=\pi r^{2}h\)
\(h=\frac{360}{\pi r^{2}}\)
\(S=2\pi rh+2\pi r^{2}\)
\(S=2\pi r\left ( \frac{360}{\pi r^{2}} \right )+2\pi r^{2}\)
\(S=2\left ( \frac{360}{r} \right )+2\pi r^{2}\)
\(S=720r^{-1}+2\pi r^{2}\)
\(\frac{\mathrm{d} S}{\mathrm{d} r}=-720r^{-2}+4\pi r\)
\(0=\frac{-720}{r^{2}}+4\pi r\)
\(4\pi r=\frac{720}{r^{2}}\)
\(4\pi r^{3}=720\)
\(r^{3}=\frac{720}{4\pi }\)
\(r^{3}=\frac{180}{\pi }\)
\(r=\sqrt[3]{\frac{180}{\pi }}\)
r=3.86cm
\(h=\frac{360}{\pi r^{2}}=\frac{360}{\pi (3.86cm)^{2}}=7.72cm\)
(C) \(S=2\pi rh+2\pi r^{2}\)
\(S=2\pi (3.86cm)(7.71cm)+2\pi (3.86cm)^{2}\)
\(S=187cm^{2}+94cm^{2}\)
\(S=281cm^{2}\)
Question
| t (minutes) | 0 | 2 | 5 | 9 | 10 |
| H(t) (degrees Celsius) | 66 | 60 | 52 | 44 | 43 |
As a pot of tea cools, the temperature of the tea is modeled by a differentiable function H for 0 ≤ t ≤ 10, where time t is measured in minutes and temperature H(t) is measured in degrees Celsius. Values of H(t) at selected values of time t are shown in the table above.
(a) Use the data in the table to approximate the rate at which the temperature of the tea is changing at time t = 3.5. Show the computations that lead to your answer.
(b) Using correct units, explain the meaning of \(\frac{1}{10}\int_{0}^{10}H(t)dt\) in the context of this problem. Use a trapezoidal sum with the four subintervals indicated by the table to estimate \(\frac{1}{10}\int_{0}^{10}H(t)dt.\)
(c) Evaluate \(\int_{0}^{10}H'(t)dt.\) Using correct units, explain the meaning of the expression in the context of this problem.
(d) At time t = 0, biscuits with temperature 100 0C were removed from an oven. The temperature of the biscuits at time t is modeled by a differentiable function B for which it is known that
B'(t) = – 13.84e-0.173t . Using the given models, at time t = 10, how much cooler are the biscuits than the tea?
Answer/Explanation
Ans:
(a)
\(\frac{H(5)-H(2)}{5-2}=\frac{-8}{3}\frac{0_{C}}{min}\)
(b)
\(\frac{1}{10}\int_{0}^{10}H(t)dt\approx \frac{\left [2(\frac{66+180}{2}) +3(\frac{52+60}{2})+4(\frac{44+52}{2})+1(\frac{43+44}{2}) \right ]}{10}=52.95\)
This represents the average temperature in degree Celsius of the tea over the interval 0 ≤ t ≤ 10
(c)
\(\int_{0}^{10}H'(t)dt= H(10)-H(0)=43-66=-23^{0}C\)
This expression shows the total change in temperature in degree Celsius from t = 0 to t = 10.
(d)
\(B'(t)=-13.84e^{-.173t}\)
\(B(10)=\int_{0}^{10}-13.84e^{-.173t}+100 = 100-65.817 = 34.1827\)
43-341827 = 8.817
= 88170C Celsius