Question
Let y = f(x) be a differentiable function such that \(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{x}{y}\) and f(8)=2 . What is the approximation of f (8.1) using the line tangent to the graph of f at x = 8?
A 0.4
B 2.025
C 2.4
D 6
Answer/Explanation
Question
The derivative of the function B is given by \(B′(t)=8e^{0.2\cos t}\) and B(2.2)=4.5. If the linear approximation to B(t) at t=2.2 is used to estimate B(t), at what value of t does the linear approximation estimate that B(t)=9 ?
A 0.633
B 0.941
C 2.833
D 4.400
Answer/Explanation
Ans:C
The linear approximation to B(t) at t=2.2 will be
y=B(2.2)+B′(2.2)(t−2.2). Since B′(2.2)=\(8e^{0.2\cos t}\)=7.1117, the linear approximation is
Question
The locally linear approximation of the differentiable function f at x=3 is used to approximate the value of f(3.2). The approximation at x=3.2 is an overestimate of the corresponding function value at x=3.2. Which of the following could be the graph of f ?
A 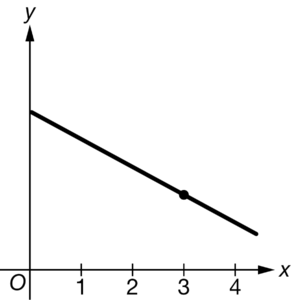
B 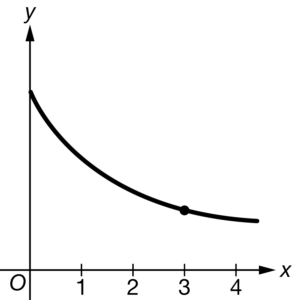
C 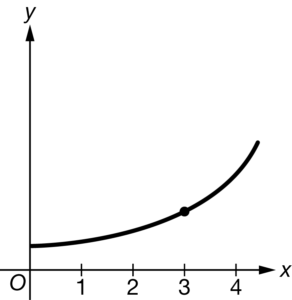
D 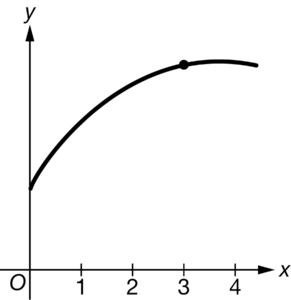
Answer/Explanation
Ans:D
Question
The line tangent to the graph of the twice-differentiable function f at the point x=3 is used to approximate the value of f(3.25). Which of the following statements guarantees that the tangent line approximation at x=3.25 is an underestimate of f(3.25) ?
A The function f is decreasing on the interval 3≤x≤3.25.
B The function f is increasing on the interval 3≤x≤3.25.
C The graph of the function f is concave down on the interval 3≤x≤3.25.
D The graph of the function f is concave up on the interval 3≤x≤3.25.
Answer/Explanation
Ans:D
