Question
| r (centimeters) | 0 | 1 | 2 | 2.5 | 4 |
| f (r) (milligrams per square centimeter) | 1 | 2 | 6 | 10 | 18 |
The density of a bacteria population in a circular petri dish at a distance r centimeters from the center of the dish is given by an increasing, differentiable function f , where f (r) is measured in milligrams per square centimeter. Values of f (r) for selected values of r are given in the table above.
(a) Use the data in the table to estimate f'(2.25). Using correct units, interpret the meaning of your answer in the context of this problem.
(b) The total mass, in milligrams, of bacteria in the petri dish is given by the integral expression \(2\pi \int_{0}^{4}rf(r)dr.\) Approximate the value of \(2\pi \int_{0}^{4}rf(r)dr.\) using a right Riemann sum with the four subintervals indicated by the data in the table.
(c) Is the approximation found in part (b) an overestimate or underestimate of the total mass of bacteria in the petri dish? Explain your reasoning.
(d) The density of bacteria in the petri dish, for 1 ≤ r ≤ 4, is modeled by the function g defined by \(g(r)=2-16 \left ( cos(1.57\sqrt{r}) \right )^{3}.\) For what value of k , 1 < k < 4, is g (k) equal to the average value of g (r) on the interval 1 ≤ r ≤ 4 ?
Answer/Explanation
Ans:
(a)
\(f'(2.25)\approx \frac{f(25)-f(2)}{2.5-2}=\frac{10-6}{0.5}=\frac{4}{0.5}= 8\) milligrams per square centimeter per centimer.
The density of bacteria changes at a rate of approximately 8 milligrams per square centimeter per centimeter at distance r = 2.25 centimeters from the center of the dish.
(b)
\(2\pi \int_{0}^{4}r.f(r)dr\approx 2\pi \cdot (2\cdot 1+1+6\cdot 1\cdot 2+10\cdot 0.5\cdot 2+18\cdot 4)\)
\(=2\pi (2+12+12.5+108)=2\pi (134.5)=269\pi milligrams\)
(c)
As a rule, Right riemann sums are always an over estimate for functions with positive slope, and underestimates for functions with negative slope. The slope of r.f(r) is equal to r’.f(r) + r.f'(r). Since r, r’, f(r), and f'(r) are always positive on the interval [0, 4], r.f(r) always has a positive slope on that interval. Since it’s a positive sloped function, the right riemann sum for r.f(r) from 0 to 4 is an over estimate.
(d)
Avg of \(g(r)=\frac{1}{4-1}\int_{1}^{4}\left ( 2-16(cos (1.57\sqrt{r}) \right )^{3}dr=\frac{29.627}{3}=9.876\)
\(g(k)=2-16\left ( cos (1.57\sqrt{r}) \right )^{3}=9.876\)
k = 2.497
Question
The marginal cost of producing x units of an item is \(C'(x)=\frac{1}{4}x-2\)
(A) Find an expression for C(x), assuming the cost of producing 0 units is $2, such that C(0) = 2.
(B) Find the value of x such that the average cost is a minimum. Justify your answer.
(C) Find the cost for producing 40 units.
Answer/Explanation
(A)\(C(x)=\int C'(x)dx=\int \left ( \frac{1}{4}x-2 \right )dx=\frac{1}{8}x^{2}-2x+C=\frac{1}{8}x^{2}-2x+2\)
(B)\(\bar{C}=\frac{C(x)}{x}=\frac{x}{8}-2+\frac{2}{x}.\) Set \(\frac{\mathrm{d} \bar{C}}{\mathrm{d} x}\)equal to zero to find the minimum average cost.\( \frac{\mathrm{d} \bar{C}}{\mathrm{d} x}=\frac{1}{8}-\frac{2}{x^{2}}=0\)Solving for x, one obtains x = 4. Find the second derivative at this point to confirm it’s a relative minimum:\(\frac{\mathrm{d} ^{2}\bar{C}}{\mathrm{d} x^{2}}=\frac{4}{x^{3}}\).At x = 4, this second derivative is positive; therefore, it is concave up and a relative minimum. The value of x such that the average cost is a minimum is 4.
(C)\(C(40)=\frac{40^{2}}{8}-2(40)+2=122\)
Question
A virus population is growing at a rate of \(P'(t)=10t-2\sqrt{t}+100\) organisms per hour every t hours.
(A) If the initial population, P(0), is 500, what is the population after t hours?
(B) What is the increase in population after 3 hours, rounded to the nearest whole number?
(C) What is the average rate of change in the population during first 12 hours?
Answer/Explanation
Question
The rate of change in temperature of a greenhouse from 7 p.m. to 7 a.m. is given by the function: \(f(t)=-3\sin \left ( \frac{t}{3} \right )\) where temperature is measured in degrees Fahrenheit and t is the number of hours after 7 p.m.
(A) If at 7 p.m. the temperature is 1058F, find the temperature of the greenhouse at 2 a.m.
(B) Write an integral expression to represent the temperature of the greenhouse at time t, where t is between 7 p.m. and 7 a.m.
(C) Find the average change in temperature of the greenhouse between 7 p.m. and 7 a.m. to the nearest 10th of a degree.
(D) Is there a point during the night when the rate of change it temperature of the greenhouse is the average change in temperature from part (c)? If yes, state the time. Either way, show all work to justify your answer.Ans:
Answer/Explanation
(A)F(0)=105,f(t) represents the rate of change of the temperature, and 2 a.m. is 7h after 7p.m.
\(F(7)=105+\int_{0}^{7}(-3\sin (t/3))dt\Rightarrow F(7)=105+9\cos (t/3)|^{7}_{0}\Rightarrow F(7)\approx 89.78\)
(B)\(F(t)=105+\int_{0}^{t}(-3\sin (x/3))dx\)
(C) Average value=\(\frac{1}{12-0}\int_{0}^{12}(-3\sin (t/3))dt\approx -1.24^{\circ}F/hour\)
(D) Since f(t) is continuous on [0, 12], by the Mean Value Theorem for integrals there
exists a number c in [0, 12] such that \(\int_{0}^{12}f(t)dt=f(c)(b-a)\)
You can use our solution from part (d) to show that f(c)=-1.24. Now solve for c.
\(f(c)=-1.24\Rightarrow -3\sin (t/3)=-1.24\Rightarrow \sin (t/3)=0.413\Rightarrow t/3=\sin ^{-1}(0.413)\Rightarrow t\approx 1.28\)
Approximately 1.28 h after 7 p.m., the rate of change of the temperature in the greenhouse equals the average rate of change of the temperature for the night. Now convert 0.28 to minutes to find the time.
\((0.28h)\times (60)=16.8min\approx 17 min\)
Question
A water barrel containing 200 gal of water is punctured and begins to leak at a rate of \( 15\sin \left ( \frac{\pi t}{30} \right )\) gal/min, where t is measured in minutes and 0 ≤ t ≤ 15.
(A) How much water to the nearest gallon leaked out after t = 7 min?
(B) What is the average amount of water leaked out per minute from t = 0 to t = 7 to the nearest gallon?
(C) Write an expression for f (t) to represent the total amount of water in the barrel at time t, where 0 ≤ t ≤ 15.
(D) At what value of t to the nearest minute will there be 100 gal of water remaining in the barrel?
Answer/Explanation
(A) The amount of water leaked out after 7 min:
\(\int_{0}^{7}15\sin \left ( \frac{\pi t}{30} \right )dt=\frac{-15\cos \left ( \frac{\pi t}{30} \right )}{\pi /30}=-\frac{450}{\pi }\cos \left ( \frac{\pi t}{30} \right )|^{7}_{0}\simeq 36.7918\)
After 7 min, approximately 37 gal have leaked out of the water barrel.
(B) The average amount of water leaked out per minute from t = 0 to t = 7:
\(\frac{1}{7-0}\int_{0}^{7}15\sin \left ( \frac{\pi t}{30} \right )dt\approx \frac{1}{7}(36.7918)\approx 5.255\approx 5 gal\)
(C) The amount of oil in the drum at time t:
\(f(t)=200-\int_{0}^{7}15\sin \left ( \frac{\pi x}{30} \right )dx\)
(D) Let a be the value of t and solve the following equation for a:
\(100=200-\int_{0}^{a}15\sin \left ( \frac{\pi t}{30} \right )dt\)
\(100=200-\left ( -\frac{450}{\pi }\cos \left ( \frac{\pi t}{30} \right ) |^{a}_{0}\right )\)
\(100=200-\left ( -\frac{450}{\pi } \cos \left ( \frac{\pi a}{30} \right )–\frac{450}{\pi }\cos \left ( \frac{\pi (0)}{30} \right )\right )\)
\(100=200+\frac{450}{\pi }\cos \left ( \frac{\pi a}{30} \right )-\frac{450}{\pi }\Rightarrow \cos \left ( \frac{\pi a}{30} \right )\approx 0.302\)
\(\frac{\pi a}{30}\approx \cos ^{-1}(0.302)\approx 1.264\Rightarrow a\approx 12.07\)
After approximately 12 min, there will be 100 gal left in the water barrel.
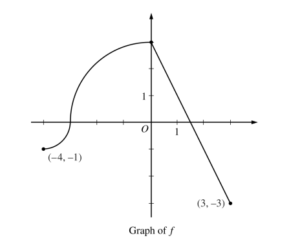
Question
The continuous function f is defined on the interval \(-4\leq x\leq 3.\) The graph of f consists of two quarter circles and one line segment, as shown in the figure above. Let \(g(x)=2x+\int_{0}^{x}f(t)dt.\)
(a) Find g(-3). Find g’(x) and evaluate g’(-3).
(b) Determine the x-coordinate of the point at which g has an absolute maximum on the interval \(-4\leq x\leq 3.\)
(c) Find all values of x on the interval -4 < x < 3 for which the graph of g has a point of inflection. Give a reason for your answer. (d) Find the average rate of change of f on the interval \(-4\leq x\leq 3.\) There is no point c, -4 < c < 3, for which f’(c) is equal to that average rate of change. Explain why this statement does not contradict the Mean Value Theorem.
Answer/Explanation
Ans:
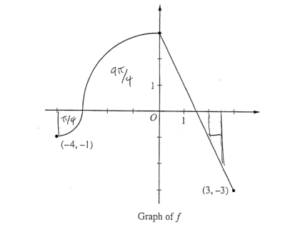
(a)
\(g(-3)=2\cdot (-3)+\int_{0}^{-3}f(t)dt=-6-\frac{9\pi }{4}\)
\(g'(x)=d/dx \left ( 2x+\int_{0}^{x}f(t)dt \right )=2+f(x)\)
g'(-3) = 2 + f(-3) = 2 + 0 = 2
(b)
g'(x) = 0 2 + f(x) = 0
f(x) = -2
x = 5/2
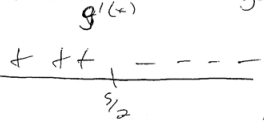
x = 5/2, because g’ check endpoints going from t to – proves it as the only relative maximum and g(5/2) is greater than g at either end point.
\(g(-4)= -8+\int_{0}^{-4}f(t)dt\)
= -8 – 2π
\(g(5/2)= 5+\int_{0}^{5/2}f(t)dt=5+\frac{5}{4}\)
\(g(3)= 6+\int_{0}^{3}f(t)dt=6\)
(c)
g”(x) = d/dx (g(x)) = f'(x)
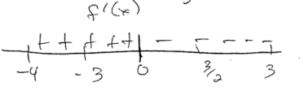
The only point of inflection for g is at x = 0, since f'(x), which is equivalent to g”, only changes signs at x = 0 on the interval -4 ≤ x ≤3
(d)
Avg. Rate of change = \(\frac{f(x)-f(-4)}{3-(-4)}\)
\(=\frac{-3–1}{3+4}=\frac{-2}{7}\)
Because Mean value Theorem only applies when the function is continuous AND differentiable on the interval, which doesn’t apply here since f(x) isn’t differentiable at x = 0.