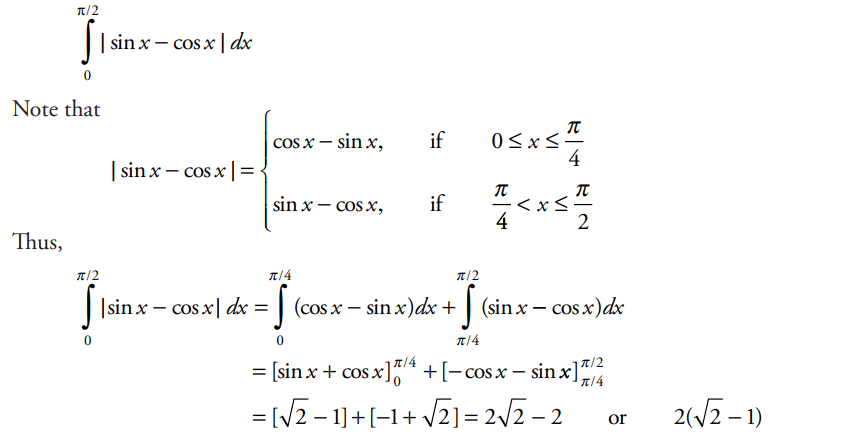Question
The area of the region between the graph of \(y= 4x^3 +2\) and the x-axis from \(x =1\) to \(x = 2\) is
(A) 36 (B) 23 (C) 20 (D) 17 (E) 9
Answer/Explanation
Ans:D
Question
The area of the region in the first quadrant enclosed by the graph of y = x(x-1 ) and the x-axis is
(A) \(\frac{1}{6}\) (B) \(\frac{1} {3}\) (C) \(\frac{2}{3}\) (D) \(\frac{5}{6}\) (E) 1
Answer/Explanation
Ans:A
Question
If you were to use 3 midpoint rectangles of equal length to approximate the area under the curve of \(f(x)=x^{2}+2\) from x = 0 to x = 3, how close would the approximation be to the exact area under the curve?
(A) \(\frac{1}{2}\)
(B) \(\frac{1}{4}\)
(C) \(\frac{1}{8}\)
(D) \(\frac{3}{4}\)
Answer/Explanation
Ans:(B)
The exact area is computed
\(\int_{0}^{3}x^{2}+2dx=\left [ \frac{x^{3}}{3} +2x\right ]^{3}_{0}=9+6=15\)
The approximation using 3 midpoint rectangles is computed
\(\sum_{i=1}^{3}f(x_{i})\left ( \frac{3-0}{3} \right )=f\left ( \frac{1}{2} \right ).1+f\left ( \frac{3}{2} \right ).1+f\left ( \frac{5}{2} \right ).1=\frac{9}{4}+\frac{17}{4}+\frac{33}{4}=\frac{59}{4}\) or 14.75
Question
Find the exact area of the region bounded by the graph of \(f(x)=\sin x\) , \(g(x)=\cos x \), and the lines x = 0 to x = π/2.
(A) \(\sqrt{2}\)
(B) 1
(C) \(\sqrt{2}-2\)
(D) \(2(\sqrt{2}-1)\)
Answer/Explanation
Ans:(D)
The area of this region may be attained by computing