Question
The area of the closed region bounded by the polar graph of \(r=\sqrt{3+cos\Theta }\) is given by the integral
(A)\(\int_{0}^{2\pi }\sqrt{3+cos\Theta } d\Theta\) (B)\(\int_{0}^{\pi }\sqrt{3+cos\Theta } d\Theta\) (C)\(2\int_{0}^{\pi /2}(3+cos\theta )d\Theta\) (D)\(\int_{0 }^{\pi}(3+cos\Theta )d\Theta\) (E)\(2\int_{0}^{\pi /2}\sqrt{3+cos\Theta }d\Theta\)
Answer/Explanation
Ans:D
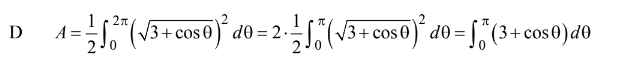
Question
The area of the region enclosed by the polar curve r =1 -cos θ is
(A)\( \frac{3}{4}\pi \) (B)\(\pi \) (C)\(\frac{3}{2}\pi\) (D)\(2\pi\) (E)\(3\pi\)
Answer/Explanation
Ans:C
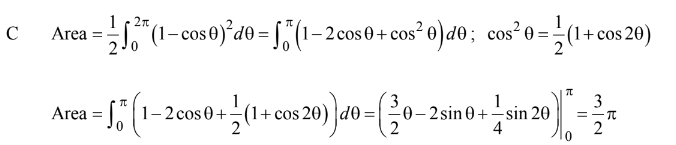
Question
The area of the region enclosed by the polar curve \(r=sin(2\Theta )for 0\leq \Theta \leq \frac{\pi }{2}\) is
(A) 0 (B) \(\frac{1}{2}\) (C) 1 (D)\(\frac{π}{8}\) (E) \(\frac{π}{4}\)
Answer/Explanation
Ans:D
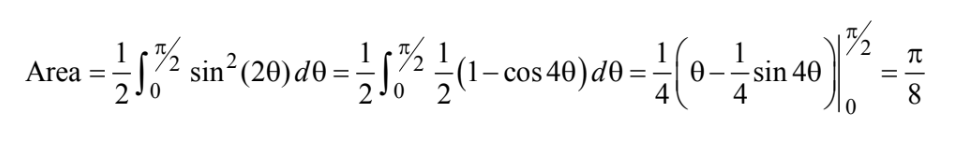
Question
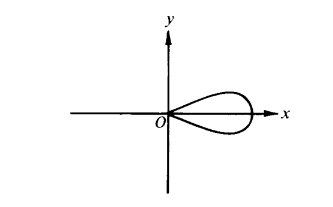
Which of the following gives the area of the region enclosed by the loop of the graph of the polar curve r =4cos(3 θ ) shown in the figure above?
(A)\(16\int_{\frac{\pi}{3}}^{\frac{\pi}{3}} cos(3\theta )d\theta\)
(B)\(16\int_{\frac{\pi}{6}}^{\frac{\pi}{6}} cos(3\theta )d\theta\)
(C)\(16\int_{\frac{\pi}{3}}^{\frac{\pi}{3}} cos^{2}(3\theta )d\theta\)
(D)\(16\int_{\frac{\pi}{6}}^{\frac{\pi}{6}} cos^{2}(3\theta )d\theta\)
(E)\(16\int_{\frac{\pi}{3}}^{\frac{\pi}{3}} cos^{2}(3\theta )d\theta\)
Answer/Explanation
Ans:E
\(r=0\) when \(cos 3\theta =0\Rightarrow \theta =\pm \frac{\pi }{6}\). The region is for the interval from \(\theta =- \frac{\pi }{6}\) to \(\theta= \frac{\pi }{6}\) .
