Question

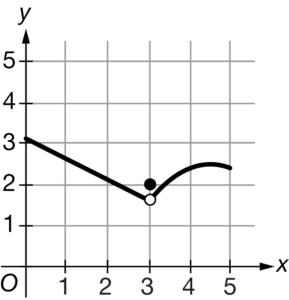
The table above gives selected values for a function
. Also shown is a portion of the graph of
. The graph consists of a line segment for x<3 and part of a parabola for x>3. What is \(\lim_{x\rightarrow 3}f(x)\)?
A 1.6
B \(\frac{1.601+1.602}{2}\)
C 2
D The limit does not exist
Answer/Explanation
Ans:A
The graph of f indicates that the limit exists at x=3 and has a value between 1 and 2. The linear segment in the graph of f has slope \(\frac{1.625-1.650}{2.95-2.9}=-\frac{0.025}{0.05}=-\frac{1}{2}\) .
The equation of the line is \(y=-\frac{1}{2}(x-2.9)+1.65\).Therefore,
Question
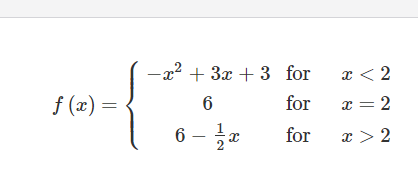
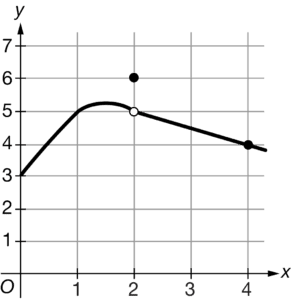
Let f be the piecewise function defined above. Also shown is a portion of the graph of f. What is the value of \(\lim_{x\rightarrow 2}f(f(x))\)?
A -15
B -7
C 3
D \(\frac{7}{2}\)
Answer/Explanation
Ans:D

Question

The table above gives selected values for a function f. Based on the data in the table, which of the following could not be the graph of
on the interval 2.9≤x≤3.1?
A 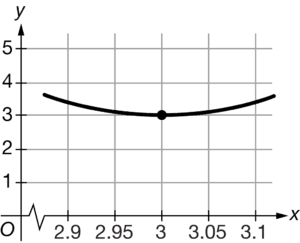
B 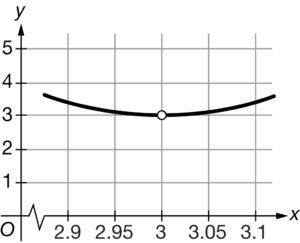
C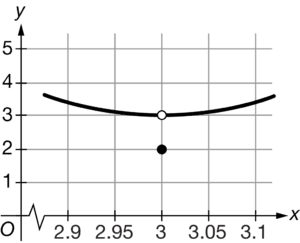
D 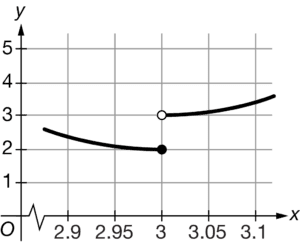
Answer/Explanation
Ans:D
The data in the table suggest that \(\lim_{x\rightarrow 3}f(x)=3\). This function has a jump discontinuity at where the limit does not exist. Therefore, this could not be the graph of
