Question
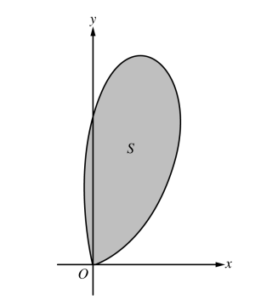
Let S be the region bounded by the graph of the polar curve \(r(\theta )=3\sqrt{\theta }sin\theta (\theta ^{2})~for~ 0\leq \theta \leq \sqrt{\pi },\) as shown in the figure above.
(a) Find the area of S.
(b) What is the average distance from the origin to a point on the polar curve \(r(\theta )=3\sqrt{\theta }sin\theta (\theta ^{2})~for~ 0\leq \theta \leq \sqrt{\pi }\)?
(c) There is a line through the origin with positive slope m that divides the region S into two regions with equal areas. Write, but do not solve, an equation involving one or more integrals whose solution gives the value of m.
(d) For k > 0, let A(k) be the area of the portion of region S that is also inside the circle r = k cos θ. Find \(\lim_{k\rightarrow \infty }A(k).\)
Answer/Explanation
Ans:
(a) \(\frac{1}{2}\int_{0}^{\sqrt{\pi }}(r(\theta ))^{2}d\theta =3.534292\)
The area of S is 3.534
(b) \(\frac{1}{\sqrt{\pi }-0}\int_{0}^{\sqrt{\pi }}r(\theta )d\theta =3.534292\)
The average distance from the origin to a point on the curve r = r(θ) for 0 ≤ θ ≤ \(\sqrt{\pi }\) is 1.580 (or 1.579).
(c) \(tan\theta =\frac{y}{x}=m\Rightarrow \theta =tan^{-1}m\)
\(\frac{1}{2}\int_{0}^{tan^{-1}m}(r(\theta ))^{2}d\theta =\frac{1}{2}\left ( \frac{1}{2}\int_{0}^{\sqrt{\pi }}(r(\theta ))^{2}d\theta \right )\)
(d) As k →∞, the circle r = k cos θ grows to enclose all points to the right of the y -axis.
\(\lim_{k\rightarrow \infty }A(k)=\frac{1}{2}\int_{0}^{\pi /2}(r(\theta ))^{2}d\theta\)
\(=\frac{1}{2}\int_{0}^{\pi /2}(3\sqrt{\theta }sin(\theta^{2} ))^{2}d\theta\)
Question
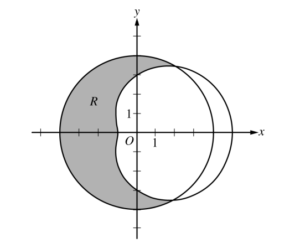
The graphs of the polar curves r = 4 and r = 3 + 2 cos θ are shown in the figure above. The curves intersect at \(\) and \(\).
(a) Let R be the shaded region that is inside the graph of r = 4 and also outside the graph of r = 3 + 2 cos θ, as shown in the figure above. Write an expression involving an integral for the area of R.
(b) Find the slope of the line tangent to the graph of r = 3 + 2 cos θ at \(\theta =\frac{\pi }{2}.\).
(c) A particle moves along the portion of the curve r = 3 + 2 cos θ for \(0<\theta <\frac{\pi }{2}.\) The particle moves in such a way that the distance between the particle and the origin increases at a constant rate of 3 units per second. Find the rate at which the angle θ changes with respect to time at the instant when the position of the particle corresponds to \(\theta =\frac{\pi }{3}.\) Indicate units of measure.
Answer/Explanation
Ans:
(a) \(Area = \frac{1}{2}\int_{\pi /3}^{5\pi /3}\left ( 4^{2}-(3+2cos\theta )^{2} \right )d\theta \)
(b) \(\frac{dr}{d\theta }=-sin\theta \Rightarrow \frac{dr}{d\theta }|_{\theta =\pi /2}=-2\)
\(r\left ( \frac{\pi }{2} \right )=3+2cos\left ( \frac{\pi }{2} \right )=3\)
\(y = r sin\theta \Rightarrow \frac{dy}{d\theta }=\frac{dr}{d\theta }sin\theta +rcos\theta \)
\(x = r cos\theta \Rightarrow \frac{dy}{d\theta }=\frac{dr}{d\theta }cos\theta +rsin\theta \)
\(\frac{dy}{dx}|_{\theta =\pi /2}=\frac{dy/d\theta }{dx/d\theta }|_{\theta =\pi /2}=\frac{-2sin\left ( \frac{\pi }{2} \right )+3cos\left ( \frac{\pi }{2} \right )}{-2cos\left ( \frac{\pi }{2} \right )-3sin\left ( \frac{\pi }{2} \right )}=\frac{2}{3}\)
The slope of the line tangent to the graph of r = 3 + 2cos θ at \(\theta =\frac{\pi }{2}is \frac{2}{3}.\)
– OR –
\(y = r sin \theta =(3+2cos\theta )sin\theta \Rightarrow \frac{dy}{d\theta }=3 cos\theta +2cos^{2}\theta -2sin^{2}\theta \)
\(x = r cos \theta =(3+2cos\theta )cos\theta \Rightarrow \frac{dx}{d\theta }=-3 sin\theta -4sin\theta cos\theta \)
\(\frac{dy}{dx}|_{\theta =\pi /2}=\frac{dy/d\theta }{dx/d\theta }|_{\theta =\pi /2}=\frac{3cos\left ( \frac{\pi }{2} \right )+2cos^{2}\left ( \frac{\pi }{2} \right )-2sin^{2}\left ( \frac{\pi }{2} \right )}{-3sin\left ( \frac{\pi }{2} \right )-4sin\left ( \frac{\pi }{2} \right )cos\left ( \frac{\pi }{2} \right )}=\frac{2}{3}\)
The slope of the line tangent to the graph of r = 3 + 2cos θ at \(\theta =\frac{\pi }{2}\) is \(\frac{2}{3}.\)
(c) \(\frac{dr}{dt}=\frac{dr}{d\theta }\cdot \frac{d\theta }{dt}=-2sin\theta \cdot \frac{d\theta }{dt}\Rightarrow \frac{dr}{dt}\cdot \frac{1}{-2sin\theta }\)
\(\frac{d\theta }{dt}|_{\theta =\pi /3}=3\cdot \frac{1}{-2sin\left ( \frac{\pi }{3} \right )}=\frac{3}{-\sqrt{3}}=-\sqrt{-3}\) radians per second
Question
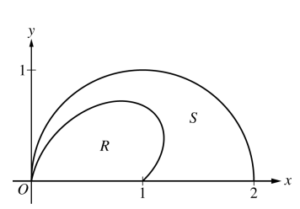
The figure above shows the polar curves r = f (θ) q = 1+ sin θ cos (2θ) and r = g(θ) = 2 cos θ for \(\(0 \leq \theta \leq \frac{\pi }{2}.\)\) Let R be the region in the first quadrant bounded by the curve r = f (θ) and the x-axis. Let S be the region in the first quadrant bounded by the curve r = f (θ) , the curve r = g (θ), and the x-axis.
(a) Find the area of R.
(b) The ray θ = k, where \(0 < k < \frac{\pi }{2},\) divides S into two regions of equal area. Write, but do not solve, an equation involving one or more integrals whose solution gives the value of k.
(c) For each θ, \(0 \leq \theta \leq \frac{\pi }{2},\) let w(θ) be the distance between the points with polar coordinates (f(θ), θ) and (g(θ), θ). Write an expression for w(θ). Find wA, the average value of w(θ) over the interval \(0 \leq \theta \leq \frac{\pi }{2}.\)
(d) Using the information from part (c), find the value of θ for which w(θ) = wA. Is the function w (θ) increasing or decreasing at that value of θ ? Give a reason for your answer.
Answer/Explanation
Ans:
(a) \(\frac{1}{2}\int_{0}^{\pi /2}(f(\theta ))^{2}d\theta =0.648414\)
The area of R is 0.648.
(b) \(\int_{0}^{k}(g(\theta ))^{2}-(f(\theta ))^{2}d\theta =\frac{1}{2}\int_{0}^{\pi /2}(g(\theta ))^{2}-(f(\theta ))^{2}d\theta\)
-OR-
\(\int_{0}^{k}(g(\theta ))^{2}-(f(\theta ))^{2}d\theta =\int_{0}^{\pi /2}(g(\theta ))^{2}-(f(\theta ))^{2}d\theta\)
(c) w(θ) = g(θ) – f(θ)
\(w_{A}=\frac{\int_{0}^{\pi /2}w(\theta )d\theta }{\frac{\pi }{2}-0}=0.485446\)
The average value of w(θ ) on the interval \(\left [ 0, \frac{\pi }{2} \right ]\) is 0.485.
(d) \(w(\theta )=w_{A}for 0\leq \theta \leq \frac{\pi }{2}\Rightarrow \theta =0.517688\)
w(θ) = wA at θ = 0.518 (or 0.517).
w'(0.518) < 0 ⇒ w(θ) is decreasing at θ = 0.518.
Question
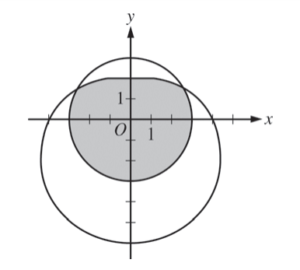
The graphs of the polar curves r = 3 and r = 4 – 2sin θ are shown in the figure above. The curves intersect when \(\theta =\frac{\pi }{6}\) and \(\theta =\frac{5\pi }{6}\).
(a) Let S be the shaded region that is inside the graph of r = 3 and also inside the graph of r = 4 – 2sin θ. Find the area of S.
(b) A particle moves along the polar curve r = 4 – 2sin θ so that at time t seconds, θ = t2 . Find the time t in the interval 1 ≤ t ≤ 2 for which the x-coordinate of the particle’s position is -1.
(c) For the particle described in part (b), find the position vector in terms of t. Find the velocity vector at time t = 1.5.
Answer/Explanation
Ans:
(a) Area = \(6\pi +\frac{1}{2}\int_{\pi /6}^{5\pi /6}(4-2sin\theta )^{2}d\theta =24.702 (or 24.708)\)
(b) x = r cos θ ⇒ x(θ) = (4 – 2 sin θ) cos θ
x(t) = (4 – 2 sin(t2)) cos (t2)
x(t) = -1 when t = 1.428 (or 1.427)
(b) y = r sin θ ⇒ y (θ) = (4 – 2 sinθ) sin θ
y(t) = (4 – 2 sin(t2)) sin (t2)
Position vector = <x(t), y (t)>
\(=\left \langle \left ( 4-2 sin (t^{2}) \right )cos (t^{2}),(4-2 sin (t^{2}))sin(t^{2}) \right \rangle\)
v(1.5) = <x'(1.5), y'(1.5)>
= <-8.072, -1.673> (or <-8.072, -1.672>)
Question
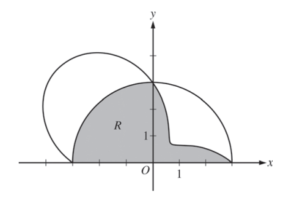
The graphs of the polar curves r =3 and r = 3 – 2sin (2θ) are shown in the figure above for 0 ≤ θ ≤ π.
(a) Let R be the shaded region that is inside the graph of r 3 and inside the graph of r = 3 – 2sin (2θ). Find the area of R.
(b) For the curve r = 3 – 2sin (2θ), find the value of \(\frac{dx}{d\theta }at \theta =\frac{\pi }{6}.\)
(c) The distance between the two curves changes for \(0< \theta < \frac{\pi }{2}.\) Find the rate at which the distance between the two curves is changing with respect to θ when \(\theta =\frac{\pi }{3}.\)
(d) A particle is moving along the curve r = 3 – 2sin (2θ) so that \(\frac{d\theta }{dt}=3\) for all times t ≥ 0. Find the value of \(\frac{dr}{dt}at \theta =\frac{\pi }{6}.\)
Answer/Explanation
Ans:
(a) \(Area = \frac{9\pi }{4}+\frac{1}{2}\int_{0}^{\pi /2}(3-2sin(2\theta ))^{2}d\theta \)
= 9.708 (or 9.707)
(b) x = (3 – 2 sin (2θ)) cos θ
\(\frac{dx}{d\theta }|_{\theta =\pi /6}=-2.366\)
(c) The distance between the two curves is
D =3− (3 – 2sin (2θ)) = 2 sin (2θ ).
\(\frac{dD}{d\theta }|_{\theta =\pi /3}=-2\)
(d) \(\frac{dr}{dt}=\frac{dr}{d\theta }\cdot \frac{d\theta }{dt}=\frac{dr}{d\theta }\cdot 3\)
\(\frac{dr}{d\theta }|_{\theta =\pi /6}=(-2)(3)=-6\)
Question
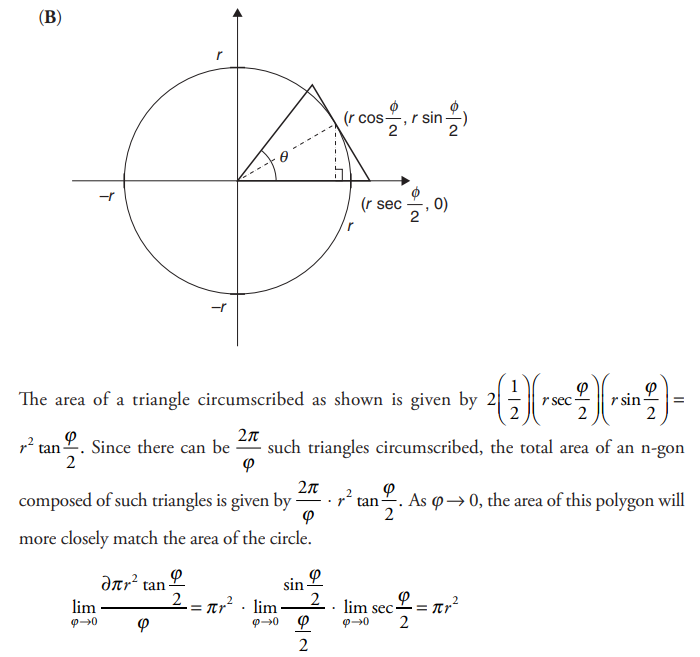
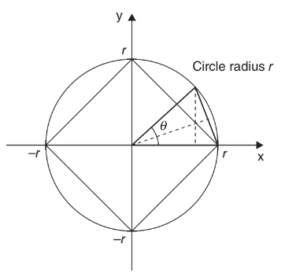
(A) Use a limit to verify the formula for the area of a circle using inscribed n-gons.
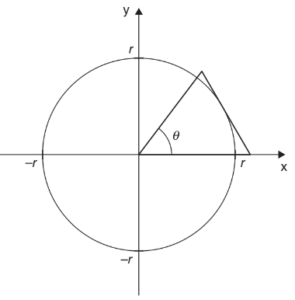
(B) Use a limit to verify the formula for the area of a circle using circumscribed n-gons.
Answer/Explanation
(A) The area of a triangle inscribed as shown is given by \(\frac{1}{2}bh=\frac{1}{2}r^{2}\sin \Theta \).Since there
can be \(\frac{2\pi }{\Theta }\) triangles of the same size inscribed in the circle, the total area of the n-gon is given by \(\frac{2\pi }{\Theta }.\frac{r^{2}\sin \Theta }{2}\). As θ→ 0, the area of this polygon will more closely match the area of the circle.
\(\lim_{\Theta \rightarrow 0}\frac{\pi r^{2}\sin \Theta }{\Theta }=\pi r^{2}\frac{\sin \Theta }{\Theta }=\pi r^{2}\)