Question
Let y = f(x) be the particular solution to the differential equation \(\frac{dy}{dx}=y\cdot (x In x)\) with initial condition f(1) = 4 . It can be shown that f”(1) = 4.
(a) Write the second-degree Taylor polynomial for f about x = 1. Use the Taylor polynomial to approximate f(2) .
(b) Use Euler’s method, starting at x = 1 with two steps of equal size, to approximate f(2) . Show the work that leads to your answer.
(c) Find the particular solution y = f(x) to the differential equation \(\frac{dy}{dx}=y\cdot (x In x)\) with initial condition f(1) = 4 .
Answer/Explanation
Ans:
(a)
\(\frac{dy}{dx}= 4.1 In 1\)
\(P_{2}(x)=4+In 1 (x-1)+\frac{4(x-1)^{2}}{2!}\) \(P_{2}(x)=4+\frac{4(x-1)^{2}}{2!}\)
\(P_{2}(2)=4+\frac{4(2-1)^{2}}{2!}= 4+2 = 6\)
(b)
\(\frac{dy}{dx}= 4\cdot 1.5 In 1.5\)
6 In 1.5
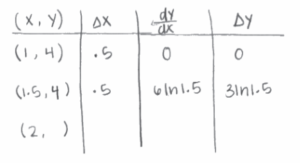
f(2) = 4 + 3 In 1.5
(c)
\(\frac{dy}{dx}= y\cdot sin x\)
\(\frac{1}{y}dy= x In x dx\) u = In x dv = x dx
\(\int \frac{1}{y}dy= \int x In x dx\) \(du = \frac{1}{x}dx\) \(v = \frac{1}{x}x^{2}\)
\(In y = \frac{1}{2}x^{2}In x -\frac{1}{4}x^{2}+ c\)
\(In 4 = \frac{1}{2}In 1 -\frac{1}{4}+ c\)
\(In 4 + \frac{1}{4}= c\)
\(In y =\frac{1}{2}x^{2}In x- \frac{1}{4}x^{2}+In 4 + \frac{1}{4}\)
\(y =4e^{\frac{1}{2}x^{2}In x}- \frac{1}{4}x^{2} + \frac{1}{4}\)
Question:
| t (minutes) |
0 | 1 | 2 | 3 | 4 | 5 | 6 |
| C (t) (ounces) |
0 | 5.3 | 8.8 | 11.2 | 12.8 | 13.8 | 14.5 |
Hot water is dripping through a coffeemaker, filling a large cup with coffee. The amount of coffee in the cup at time t, 0 ≤ t ≤ 6, is given by a differentiable function C, where t is measured in minutes. Selected values of C (t), measured in ounces, are given in the table above.
(a) Use the data in the table to approximate C'(3.5) . Show the computations that lead to your answer, and indicate units of measure.
(b) Is there a time t, 2 ≤ t ≤ 4 at which C’ (t)= 2 ? Justify your answer.
(c) Use a midpoint sum with three subintervals of equal length indicated by the data in the table to approximate the value of \(\frac{1}{6}\int_{0}^{6}C(t)dt.\) Using correct units, explain the meaning of \(\frac{1}{6}\int_{0}^{6}C(t)dt\) in the context of the problem.
(d) The amount of coffee in the cup, in ounces, is modeled by \(B(t)= 16-16e^{-0.4t}\). Using this model, find the rate at which the amount of coffee in the cup is changing when t = 5.
Answer/Explanation
Ans:
(a)
\(C'(3.5)\approx \frac{\left ( (4)-(3) \right )}{4-3}=\frac{12.8-11.2}{1}=1.6\frac{08}{min}\)
(b)
Since C(t) is differentiable for all values is [2, 4], we can say that there must be some value of t in (2, 4), such as t = a, such that \(C'(a)=\frac{\left ( (4)-(2) \right )}{4-2}=\frac{12.8-8.8}{2}=2\) by the mean value theorem
so, yes’.
(c)
\(\frac{1}{6}\int_{0}^{6}C(t)dt \approx \frac{1}{6}-2.(5.3+11.2+13.8)\)
≈ 10.1 0t
This is the average value, in oz, of the amount of coffee in the cup over the interval 0 ≤ t ≤ 6.
(d)
\(B'(t)= \frac{32}{5}e^{-0.4t}\)
\(B'(5)= \frac{32}{5}e^{-2}\)
Question
Consider the differential equation \(\frac{dy}{dx}=y^{2}(2x+2).\) Let y = f(x) be the particular solution to the differential equation with initial condition f (0)= -1.
(a) Find \(\lim_{x\rightarrow 0}\frac{f(x)+1}{sinx}.\) Show the work that leads to your answer.
(b) Use Euler’s method, starting at \(x_ 0\) with two steps of equal size, to approximate \(f\left ( \frac{1}{2} \right )\).
(c) Find y = f(x), the particular solution to the differential equation with initial condition f(0) = – 1.
Answer/Explanation
Ans:
(a) \(\lim_{x\rightarrow 0}(f(x)+1)=-1+1=0 and \lim_{x\rightarrow 0} sin x = 0\)
Using L’Hospital’s Rule,
\(\lim_{x\rightarrow 0}\frac{f(x)+1}{sinx}=\lim_{x\rightarrow 0} \frac{f'(x)}{cos x}=\frac{f'(0)}{cos 0}=\frac{(-1)^{2}\cdot 2}{1}=2\)
(b) \(f\left ( \frac{1}{4} \right )\approx f(0)+f'(0)\left ( \frac{1}{4} \right )\)
\(=-1+(2)\left ( \frac{1}{4} \right )=-\frac{1}{2}\)
\(f\left ( \frac{1}{2} \right )\approx f\left ( \frac{1}{4} \right )+f’\left ( \frac{1}{4} \right )\left ( \frac{1}{4} \right )\)
\(=-\frac{1}{2}+\left ( -\frac{1}{2} \right )^{2}\left ( 2\cdot \frac{1}{4}+2 \right )\left ( \frac{1}{4} \right )=-\frac{11}{32}\)
(c) \(\frac{dy}{dx}=y^{2}(2x+2)\)
\(\frac{dy}{y^{2}}=(2x+2)dx\)
\(\int \frac{dy}{y^{2}}=\int (2x+2)dx\)
\(-\frac{1}{y}=x^{2}+2x+C\)
\(-\frac{1}{-1}=0^{2}+2\cdot 0+C\Rightarrow C = 1\)
\(-\frac{1}{y}=x^{2}+2x+ 1\)
\(y=-\frac{1}{x^{2}+2x+ 1}=-\frac{1}{(x+1)^{2}}\)
Note: This solution is valid for x > -1.
Question
Consider the differential equation given by \(dy/dx=\frac{4xy}{5}\) .
(A) On the axis provided below, sketch a slope field for the given differential equation at the points indicated.
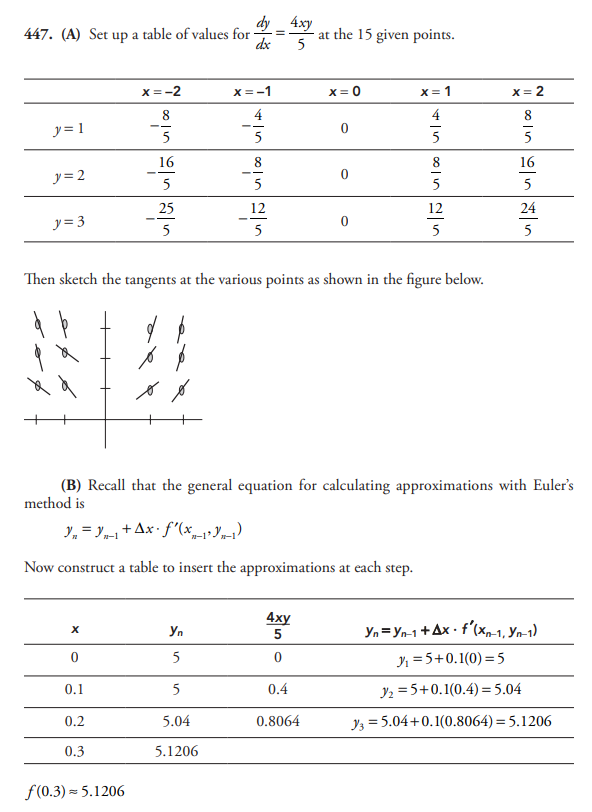
(B) Let y = f (x) be the particular solution to the given differential equation with initial condition f (0) = 5. Use Euler’s method and a step size of 0.1 to approximate f (0.3). Show the work that leads to your answer.
(C) Find the particular solution y = f (x) to the given differential equation with initial condition f (0) = 5.
(D) Use your solution above to find f (0.3).
Answer/Explanation

Question
| t (minutes) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| C(t) (ounces) | 0 | 5.3 | 8.8 | 11.2 | 12.8 | 13.8 | 14.5 |
Hot water is dripping through a coffeemaker, filling a large cup with coffee. The amount of coffee in the cup at time t, 0 ≤ t ≤ 6, is given by a differentiable function C, where t is measured in minutes. Selected values of C(t), measured in ounces, are given in the table above.
(a) Use the data in the table to approximate C'(3.5). Show the computations that lead to your answer, and indicate units of measure.
(b) Is there a time t, 2 ≤ t ≤ 4 at which C'(t) = 2 ? Justify your answer.
(c) Use a midpoint sum with three subintervals of equal length indicated by the data in the table to approximate the value of \(\frac{1}{6}\int_{0}^{6}C(t)dt.\) Using correct units, explain the meaning of \(\frac{1}{6}\int_{0}^{6}C(t)dt\) in the context of the problem.
(d) The amount of coffee in the cup, in ounces, is modeled by B(t) = 16 – 16e-0.4t. Using this model, find the rate at which the amount of coffee in the cup is changing when t = 5.
Answer/Explanation
Ans:
(a) \(C'(3.5)\approx \frac{C(4)-C(3)}{4-3}=\frac{12.8-11.2}{1}=1.6 ounces/min\)
(b) C is differentiable ⇒ C is continuous (on the closed interval) \(\frac{C(4)-C(2)}{4-2}=\frac{12.8-8.8}{2}=2\)
Therefore, by the Mean Value Theorem, there is at least
one time t, 2 < t < 4, for which C'(t)=2.
(c) \(\frac{1}{6}\int_{0}^{6}C(t)dt\approx \frac{1}{6}\left [ 2\cdot C(1)+2\cdot C(3)+2\cdot C(5) \right ]\)
\(= \frac{1}{6}(2\cdot 5.3+2\cdot 11.2+2\cdot 13.8)\)
\(= \frac{1}{6}(60.6)= 10.1 ounces\)
\(\frac{1}{6}\int_{0}^{6}C(t)dt\) is the average amount of coffee in the cup, in ounces, over the time interval 0 ≤ t ≤ 6 minutes.
(d) \(B'(t)=-16(-0.4)e^{-0.4t}=6.4e^{-0.4t}\)
\(B'(5)=6.4e^{-0.4(5)}=\frac{6.4}{e^{2}}ounces/min\)
Question
This problem is solved without a calculator. The slope of a function f at any given point (x, y) is \(\frac{2y}{3x^{2}}\) . The point (3, 4) is on the graph of f.
(A) Write an equation of the tangent line to the graph of f at x = 3.
(B) Use the tangent line in part (a) to approximate f (5). Is this approximation an overestimate or underestimate? Justify your answer using the second derivative test.
(C) Solve the separable differential equation \( \frac{\mathrm{d} y}{\mathrm{d} x}=\frac{2y}{3x^{2}}\) with initial condition f(3) = 4.
(D) Use the solution in part (c) to find f(5).
Answer/Explanation
(A) The slope at x=3 (i.e.,the point (3,4)) is
\(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{2y}{3x^{2}}\Rightarrow \frac{\mathrm{d} y}{\mathrm{d} x}=\frac{2(4)}{3(3)^{2}}=\frac{8}{27}\)
Now write the equation of the tangent line at (3, 4) in point-slope form.
\(y-y_{0}=m(x-x_{0})\Rightarrow y-4=\frac{8}{27}(x-3)\Rightarrow y=\frac{8}{27}(x-3)+4\Rightarrow y=\frac{8}{27}x+\frac{28}{9}\)
(B)\(f(5)=\frac{8}{27}(5-3)+4=\frac{124}{27}\) This is an overestimate because the graph is concavedown over the interval (3,5) with a negative second derivative of \(\left ( (3x^{2})y’-6x(2y) \right )/(3x^{2})^{2}\)
(C) Start by separating the variables and integrating both sides
\(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{2y}{3x^{2}}\Rightarrow \frac{1}{2y}dy=\frac{1}{3x^{2}}dx\Rightarrow \int \frac{1}{2y}dy=\int \frac{1}{3x^{2}}dx
\frac{1}{2}\int \frac{1}{y}dy=\frac{1}{3}\int x^{-2}dx\Rightarrow \frac{1}{2}\ln |y|=\left ( \frac{1}{3} \right )\frac{x^{-1}}{-1}+c_{1}\Rightarrow \frac{1}{2}\ln \left | y \right |=-\frac{1}{3x}+c_{1}
\ln \left | y \right |=-\frac{2}{3x}+c_{2}\Rightarrow e^{\ln \left | y \right |}=e^{-\frac{2}{3x}+c_{2}}=e^{-\frac{2}{3x}.e^{c_{2}}}\)
\(y=c_{3}e^{-\frac{2}{3x}}\)
Now use the initial condition f(3) = 4 to solve for \(c_{3}\).
\(4=c_{3}e^{-\frac{2}{3(3)}}\Rightarrow c_{3}=4.9954\)
\(y=4.9954e^{-\frac{2}{3x}}\)
(D) Evaluate the equation in C at f(5).
\(f(5)=4.9954e^{-\frac{2}{3(5)}}\approx 4.37184\)
Question
At the beginning of 2010, a landfill contained 1400 tons of solid waste. The increasing function W models the total amount of solid waste stored at the landfill. Planners estimate that W will satisfy the differential equation \( \frac{dW}{dt}=\frac{1}{25}(W-300) \) for the next 20 years. W is measured in tons, and t is measured in years from the start of 2010.
(a) Use the line tangent to the graph of W at t = 0 to approximate the amount of solid waste that the landfill contains at the end of the first 3 months of 2010 \( (time ~t = \frac{1}{4}) \)
(b) Find \(\frac{d^{2}W}{dt^{2}}\) in terms of W. Use \(\frac{d^{2}W}{dt^{2}}\) to determine whether your answer in part (a) is an underestimate or an overestimate of the amount of solid waste that the landfill contains at time \( t = \frac{1}{4}. \)
(c) Find the particular solution W = W(t) to the differential equation \(\frac{dW}{dt}=\frac{1}{25}(W-300)\) with initial condition W(0) =1400.
Answer/Explanation
Ans:
(a)
at t = 0, w = 1400
so
\(\frac{dW}{dt}|_{t=0}=\frac{1}{25}(1100)=44 tons/year = W'(0)\)
W(x+a) ≈ W(x) + aW'(x)
\(W(0+\frac{1}{4})\approx W(0)+\frac{1}{4}W'(0)\)
\(W(\frac{1}{4})\approx 1400+11\)
\(W(\frac{1}{4})\approx 1411 tons\)
There will be about 1411 tons of landfill after 3 months.
(b)
\(\frac{dW}{dt}=\frac{1}{25}W-12\) So \(\frac{d^{2}W}{dt^{2}}\) is always positive b/c W > 300.
\(\frac{d^{2}W}{dt^{2}}=\frac{1}{25}\frac{dW}{dt}\)
\(\frac{d^{2}W}{dt}=\frac{1}{625}(W-300)\)
The answer in part a is an underestimate because since \(\frac{d^{2}W}{dt^{2}}\) is always positive for t > 0, the graph of w is concave up, so the linearization of w is an underestimate.
(c)
\( \frac{dW}{dt}=\frac{1}{25}(W-300)\)
\(\int \frac{dW}{W-300}=\int \frac{1}{25}dt\)
\(e^{\xi n|W-300|}=e^{\frac{1}{25}t+c}\)
can remove abs value b/c w > 300. (iner fn)
\(|W-300|=Ce^{\frac{1}{25}t}\)
Initial condition W(0) = 1400
1400 – 300 = C e0
1100 = c
\(W-300=1100e^{\frac{1}{25}t}\)
\(W= W(t)=1100e^{\frac{1}{25}t}+300\)
Question
| x | 1 | 1.1 | 1.2 | 1.3 | 1.4 |
| f'(x) | 8 | 10 | 12 | 13 | 14.5 |
The function f is twice differentiable for x > 0 with f(1) = 15 and f”(1) = 20. Values of f’, the derivative of f, are given for selected values of x in the table above.
(a) Write an equation for the line tangent to the graph of f at x =1. Use this line to approximate f(1.4).
(b) Use a midpoint Riemann sum with two subintervals of equal length and values from the table to approximate \(\) Use the approximation for \(\) to estimate the value of f(1.4). Show
the computations that lead to your answer.
(c) Use Euler’s method, starting at x = 1 with two steps of equal size, to approximate f(1.4). Show the computations that lead to your answer.
(d) Write the second-degree Taylor polynomial for f about x = 1. Use the Taylor polynomial to approximate f(1.4).
Answer/Explanation
Ans:
(a) f(1) = 15, f'(1) = 8
An equation for the tangent line is
y = 15 + 8 (x – 1) .
f(1.4) ≈ 15 + 8 (1.4 – 1) = 18.2
(b) \(\int_{1}^{1.4}f'(x)dx\approx (0.2)(10)+(0.2)(13)=4.6\)
\(f(1.4)=f(1)+\int_{1}^{1.4}f'(x)dx\)
f(1.4) ≈ 15 + 4.6 = 19.6
(c) f(1.2) ≈ f(1) + (0.2) (8) = 16.6
f(1.4) ≈ 16.6 + (0.2) (12) = 19.0
(d) \(T_{2}(x)=15+8(x-1)+\frac{20}{2!}(x-1)^{2}\)
= 15 + 8 (x-1) + 10(x – 1)2
f(1.4) ≈ 15 + 8(1.4-1) + 10(1.4 – 1)2 = 19.8
