Question
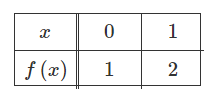
Let f be the function given by \(f(x)=2^{x^{2}}\) . Selected values of f are given in the table above. If the values in the table are used to approximate f′(0.5), what is the difference between the approximation and the actual value of f′(0.5) ?
A 0
B 0.176
C 0.824
D 1
Answer/Explanation
Ans:B
Question

The graph of the trigonometric function f is shown above for a≤x≤b. At which of the following points on the graph of f could the instantaneous rate of change of f equal the average rate of change of f on the interval [a,b] ?
A A
B B
C C
D D
Answer/Explanation
Ans:B
Question
If \( f(x)=2+|x-3|\) all x, then the value of the derivative \(f'(x)at x=3 \)is
(A) -1 (B) 0 (C) 1 (D) 2 (E) nonexistent
Answer/Explanation
Ans:E
Question
If \(y= In \left ( x^{2} +y^{2}\right )\)then the value of \(\frac{dy}{dx}\) at the point (1,0) is
(A) 0 (B)\(\frac{1}{2}\) (C) 1 (D) 2 (E) undefined
Answer/Explanation
Ans:D
