Question
What is the sum of the series \(\frac{\pi }{e}-\frac{\pi }{e^{2}}+\frac{\pi }{e^{3}}-\frac{\pi }{e^{4}}+…..+(-1)^{n+1}\frac{\pi }{e^{n}}+….?\)
A \(\frac{\pi }{e+\pi }\)
B \(\frac{\pi }{e+1}\)
C \(\frac{\pi }{e-1 }\)
D The series diverges.
Answer/Explanation
Question
The sum of the infinite geometric series \(\frac{3}{2}+\frac{9}{16}+\frac{27}{128}+\frac{81}{1,024}+\) …..is
(A) 1.60 (B) 2.35 (C) 2.40 (D) 2.45 (E) 2.50
Answer/Explanation
Ans:C
Question
\(\sum_{i=n}^{\infty }\left ( \frac{1}{3} \right )^{i}\)=
(A)\(\frac{3}{2}-\left ( \frac{1}{3} \right )^{n}\) (B)\(\frac{3}{2}\left [ 1-\left ( \frac{1}{3} \right )^{n} \right ] \) (C)\(\frac{3}{2}\left ( \frac{1}{3} \right )^{n}\) (D)\(\frac{2}{3}\left ( \frac{1}{3} \right )^{n}\) (E)\(\frac{2}{3}\left ( \frac{1}{3} \right )^{n+1}\)
Answer/Explanation
Ans:C
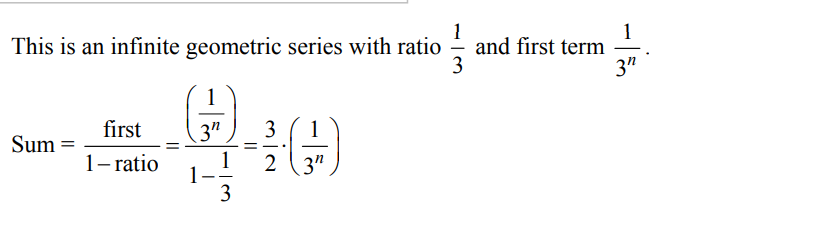
Question
Find the sum of the infinite series \(4+\frac{4}{3}+\frac{4}{9}+\frac{4}{27}\)
(A) \(\frac{85}{3}\)
(B) 24
(C) \(\frac{20}{3}\)
(D) 6
Answer/Explanation
Ans:(D)
This is a geometric series, as each term differs from the previous term by a factor of \(\frac{1}{3}\).Observe that if you let \(a_{n}=\frac{4}{3^{n-1}}\),then \(a_{1}=4,a_{2}=\frac{4}{3},a_{3}=\frac{4}{9}\) and so on. Thus, the series may be written
