Question
The length of the path described by the parametric equations \(x=cos^{3}t and y=sin^{3}t for 0\leq t\leq \frac{\pi}{2}\) is given by
(A)\(\int_{0}^{\frac{\pi}{2}}\sqrt{3cos^{2}t+3sin^{2}dt}\)
(B)\(\int_{0}^{\frac{\pi}{2}}\sqrt{-3cos^{2}t+3sin^{2}tcost}\)
(C)\(\int_{0}^{\frac{\pi}{2}}\sqrt{9cos^{4}t+9sin^{4}dt}\)
(D)\(\int_{0}^{\frac{\pi}{2}}\sqrt{9cos^{4}tsin^{2} t+9sin^{4}tcos^{2}t}dt\)
(E)\(\int_{0}^{\frac{\pi}{2}}\sqrt{cos^{6}t+sin^{6}dt}\)
Answer/Explanation
Ans:D
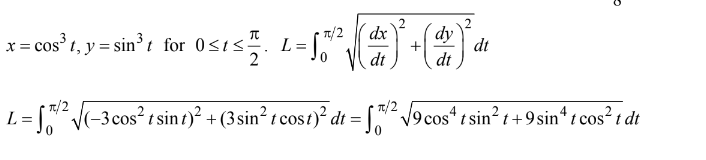
Question
The length of the path described by the parametric equations \(x=\frac{1}{3}t^3\) and \(y=\frac{1}{2}t^2 \) where\( 0\leq t\leq 1\)
(A)\(\int_{0}^{1}\sqrt{t^2+1}dt\)
(B)\(\int_{0}^{1}\sqrt{t^2+t}dt\)
(C)\(\int_{0}^{1}\sqrt{t^2+1}dt\)
(D)\(\frac{1}{2}\sqrt{4+t^4}\)
(E)\(\frac{1}{6}\int_{0}^{1}t^2\sqrt{4t^2+9}dt\)
Answer/Explanation
Ans:C
Question
A parametric curve is given by x = ln t and y = 4t + 1. Find the Cartesian equation of the curve.
(A) \(y=-\frac{1}{4\ln x}\)
(B) \(y=\frac{1}{4\ln x}\)
(C) y = 4 ln x + 1
(D) \(y=4e^{x}+1\)
Answer/Explanation
Ans:(D)
Question
Find the area underneath the curve defined by the parametric equations \(x=t+e^{t}\) and \(y=1+e^{t}\) when \(0\leq t\leq \ln 2\) .
(A) \(\ln 2+\frac{7}{2}\)
(B) \(2+\ln \left ( \frac{3}{2} \right )\)
(C) \(\ln 2-\frac{7}{2}\)
(D) \(2-\ln \left ( \frac{3}{2} \right )\)
Answer/Explanation
Ans:(C)
The area of the region is obtained by computing
\(\int_{0}^{r}\cos x-(e^{x}-1)dx=\left [ \sin x-e^{x} +x\right ]^{r}_{0}=\sin r-e^{r}+r+1\)
where r > 0 is the unique positive solution to \(\cos x=e^{x}-1\). Using a calculator to find the x-coordinate of this point of intersection yields r ≈ . 0 6013467. Therefore, substituting in for r, the area of the region is approximately 0.342526, which may be rounded to 0.343.
\(\int_{1}^{2+\ln 2}ydx=\int_{0}^{\ln 2}\left ( 1+e^{t} \right )^{2}dt=\int_{0}^{\ln 2}\left ( 1+2e^{t}+e^{2t} \right )dt\)
\(=\left [ t+2e^{t}+\frac{e^{2t}}{2} \right ]^{\ln 2}_{0}=\left ( \ln (2)+4+2 \right )-\left ( 2+\frac{1}{2} \right )=\ln 2-\frac{7}{2}\)
