Question
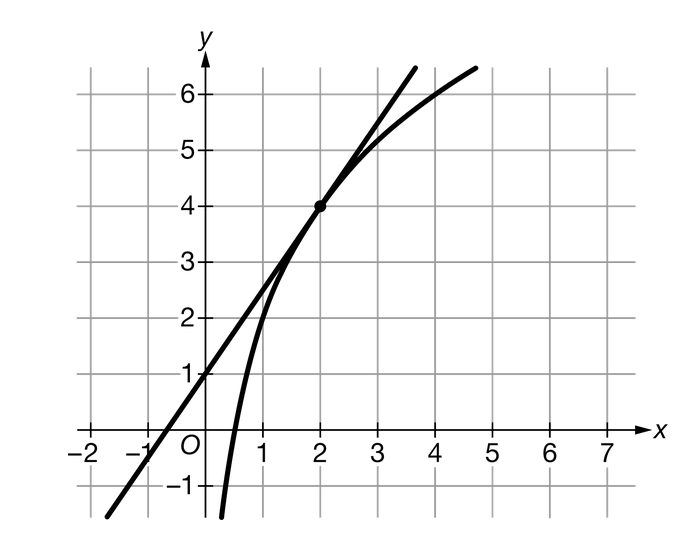
The graph of the increasing differentiable function f is shown above. Also shown is the line tangent to the graph of f at the point (2,4). Let g be the inverse of f. Which of the following statements about g′ is true?
A \({g}'(2)=\frac{2}{3}\)
B \({g}'(2)=\frac{3}{2}\)
C \({g}'(4)=\frac{2}{3}\)
D \({g}'(4)=\frac{3}{2}\)
Answer/Explanation
Ans:C
Question
Let f be the decreasing function defined by \(f(x)=−x^3−6x^2−12x+8\), where \(f(4)=−8\). If g is the inverse function of f, which of the following is a correct expression for \({g}'(−8)\) ?
A \({g}'(−8)=\frac{1}{{f}'(−8)}\)
B \({g}'(−8)=\frac{1}{{f}'(4)}\)
C \({g}'(−8)={f}'(4)\)
D \({g}'(−8)={f}'(−8)\)
Answer/Explanation
Ans:B
This can be confirmed using the chain rule and the definition of an inverse function. Since \(f(g(x))=x\)
, it follows that \(\frac{d}{dx}f(g(x))={f}'(g(x)){g}'(x)=\frac{d}{dx}(x)=1⇒{g}'(x)=\frac{1}{{f}'(g(x))}\). Therefore, \({g}'(−8)=\frac{1}{{f}'(g(−8))}=\frac{1}{{f}'(4)}\).
Question
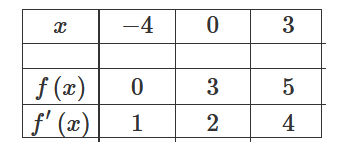
The table above gives selected values for a differentiable and increasing function f and its derivative. If \(g(x)=f^{−1}(x)\) for all x, which of the following is a correct expression for \({g}'(0)\) ?
A \({g}'(0)={f}'(0)=2\)
B \({g}'(0)=\frac{1}{{f}'(0)}=\frac{1}{2}\)
C \({g}'(0)=\frac{1}{{f}'(−4)}=1\)
D \({g}'(0)=−\frac{{f}'(0)}{(f(0))^2}=−\frac{2}{9}\)
Answer/Explanation
Ans:C
This value can be confirmed using the chain rule and the definition of an inverse function. Since \(f(g(x))=x\)
Question
If \(f(x)=\frac{\sqrt{x}}{2}\) and \(g(x)=\cos x\),find \({[f(g(x))]}’\)
(A) \(\frac{\sin x}{4\sqrt{\cos x}}\)
(B) \(-\frac{\sin x}{4\sqrt{\cos x}}\)
(C) \(-\frac{\sin x}{2\sqrt{\cos x}}\)
(D) \(\frac{\sin x\sqrt{\cos x}}{4}\)
Answer/Explanation
Ans:(B)
