Question
Suppose \(lim_{n→∞}a_n=∞\) and \(a_{n+1}≥ a_{n}> 0\) for all n≥ 1 . Which of the following statements must be true?
A \(∑_{n=1}^{∞}\frac{1}{a_n}\) diverges.
B \(∑_{n=1}^{∞}(−1)^na_n\) converges.
C \(∑_{n=1}^{∞}\frac{1}{a_n}\) converges.
D \(∑_{n=1}^{∞}\frac{(-1)^n}{a_n}\) converges.
Answer/Explanation
Question
Which of the following series converge?
I. \(\sum_{n=1}^{\infty } (-1)^{n+1}\frac{1}{2n+1}\)
II.\( \sum_{n=1}^{\infty }\frac{1}{n}\left ( \frac{3}{2} \right )^{n}\)
III.\(\sum_{n=1}^{\infty }\frac{1}{nlnn}\)
(A) I only
(B) II only
(C) III only
(D) I and III only
(E) I, II, and III
Answer/Explanation
Ans:A
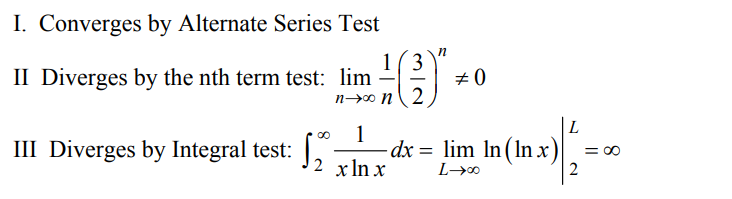
Question
What are all values of x for which the series \(\sum_{n=1}^{\infty }\frac{x^{n}}{n}\)converges?
(A)\(-1\leq x\leq 1\) (B)\(-1<x\leq 1\) (C)\(-1\leq x<1 \) (D)\(-1<x<1\) (E)All real x
Answer/Explanation
Ans:C
Question
Which of the following series are convergent?
I. \(1+\frac{1}{2^2}+\frac{1}{3^2}+………….+\frac{1}{n^2}+……….\)
II. \(1+\frac{1}{2}+\frac{1}{3}+………….+\frac{1}{n}+……….\)
III. \(1-\frac{1}{3}+\frac{1}{3^2}+………….+\frac{(-1)^{n+1}}{3^{n-1}}+……….\)
(A) I only
(B) III only
(C) I and III only
(D) II and III only
(E) I, II, and III
Answer/Explanation
Ans:C
I. convergent: p-series with p = 2>1
II. divergent: Harmonic series which is known to diverge
