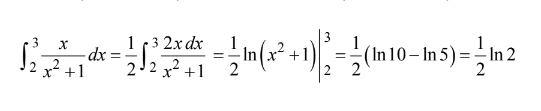Question
\(\int \frac{xdx}{\sqrt{3x^{2}+5}}\)=
(A)\(\frac{1}{9}\left ( 3x^{2}+5 \right )^{\frac{3}{2}}+C\) (B)\(\frac{1}{4}\left ( 3x^{2}+5 \right )^{\frac{3}{2}}+C\) (C)\(\frac{1}{12}\left ( 3x^{2}+5 \right )^{\frac{1}{2}}+C\) (D)\(\frac{1}{3}\left ( 3x^{2}+5 \right )^{\frac{3}{2}}+C \) (E)\(\frac{3}{2}\left ( 3x^{2}+5 \right )^{\frac{1}{2}}+C\)
Answer/Explanation
Ans:D
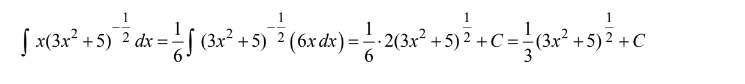
Question
\(\int_{0}^{\frac{\pi }{2}}\frac{cos\Theta }{\sqrt{1+sin\Theta }}d\Theta\)
(A)\(-2\left ( \sqrt{2}-1 \right ) \) (B)\(( -2\sqrt{2})\) (C)\(( -2\sqrt{2})\) (D)\(2(\sqrt{2}-1)\) (E)\(2(\sqrt{2}+1)\)
Answer/Explanation
Ans:D
Question
\( \int_{2}^{3}\frac{x}{x^{2}+1}dx=\)
(A)\(\frac{1}{2}ln \frac{3}{2}\) (B)\(\frac{1}{2}ln2 \) (C) ln 2 (D) 2ln 2 (E)\(\frac{1}{2}ln5\)
Answer/Explanation
Ans:B