Question
Researchers on a boat are investigating plankton cells in a sea. At a depth of h meters, the density of plankton cells, in millions of cells per cubic meter, is modeled by \(p(h)=0.2h^{2}e^{-0.0025h^{2}}\) for 0 ≤ h ≤ 30 and is modeled by f(h) for h ≥ 30. The continuous function f is not explicitly given.
(a) Find p'(25 ). Using correct units, interpret the meaning of p ‘(25) in the context of the problem.
(b) Consider a vertical column of water in this sea with horizontal cross sections of constant area 3 square meters. To the nearest million, how many plankton cells are in this column of water between h = 0 and h = 30 meters?
(c) There is a function u such that 0 ≤ f(h) ≤ u(h) for all h ≥ 30 and \(\int_{30}^{\infty }u(h)dh=105.\) The column of water in part (b) is K meters deep, where K > 30. Write an expression involving one or more integrals that gives the number of plankton cells, in millions, in the entire column. Explain why the number of plankton cells in the column is less than or equal to 2000 million.
(d) The boat is moving on the surface of the sea. At time t ≥ 0, the position of the boat is (x(t), y(t)), where x'(t)= 662 sin (5t) and y ‘ (t) = 880 cos (6t). Time t is measured in hours, and x(t) and y (t) are measured in meters. Find the total distance traveled by the boat over the time interval 0 ≤ t ≤ 1.
Answer/Explanation
Ans:
(a) p′(25) = – 1.179
At a depth of 25 meters, the density of plankton cells is changing at a rate of −1.179 million cells per cubic meter per meter.
(b) \(\int_{0}^{30}3p(h)dh=1675.414936\)
There are 1675 million plankton cells in the column of water between h = 0 and h = 30 meters.
(c) \(\int_{30}^{k}3f(h)dh\) represents the number of plankton cells, in millions, in the column of water from a depth of 30 meters to a depth of K meters. The number of plankton cells, in millions, in the entire column of water is given by \(\int_{0}^{30}3p(h)dh+\int_{30}^{k}3f(h)dh.\)
Because 0 ≤ f(h) ≤ u(h) for all h ≥30,
\(3\int_{30}^{k}f(h)dh\leq 3\int_{30}^{k}u(h)dh\leq 3\int_{30}^{\infty }=3\cdot 105=315.\)
The total number of plankton cells in the column of water is bounded by 1675.415 +315 =1990.415 ≤ 2000 million.
(d) \(\int_{0}^{1}\sqrt{(x'(t))^{2}+(y'(t))}dt=757.455862\)
The total distance traveled by the boat over the time interval 0 ≤ t ≤ 1 is 757.456 (or 757.455) meters.
Question
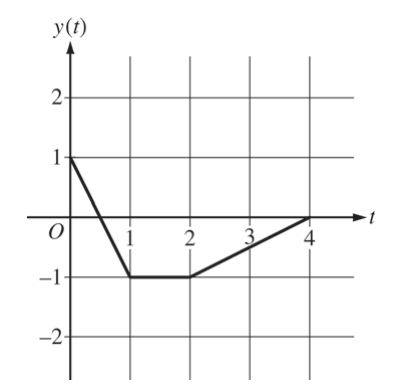
At time t, the position of a particle moving in the xy-plane is given by the parametric functions (x(t), y(t)), where \(\frac{dx}{dt}=t^{2}+sin(3t^{2}).\) The graph of y, consisting of three line segments, is shown in the figure above. At t = 0, the particle is at position (5, 1).
(a) Find the position of the particle at t = 3.
(b) Find the slope of the line tangent to the path of the particle at t = 3.
(c) Find the speed of the particle at t =3.
(d) Find the total distance traveled by the particle from t = 0 to t = 2.
Answer/Explanation
Ans:
(a) v(4) = 2.978716 > 0
v'(4) = -1.164000 < 0
The particle is slowing down since the velocity and acceleration have different signs.
(b) v(t) = 0 ⇒ t = 2.707468
v(t) changes from positive to negative at t = 2.707. Therefore, the particle changes direction at this time.
(c) \(x(0)=x(4)+\int_{4}^{0}v(t)dt\)
= 2 + (-5.815027) = -3.815
(d) \(Distance=\int_{0}^{3}v|(t)|dt=5.301\)
Question
| t (minutes) | 0 | 2 | 5 | 8 | 12 |
| vA(t) (meters/minute) | 0 | 100 | 40 | 120 | 150 |
Train A runs back and forth on an east-west section of railroad track. Train A’s velocity, measured in meters per minute, is given by a differentiable function vA(t), where time t is measured in minutes. Selected values for vA(t) are given in the table above.
(a) Find the average acceleration of train A over the interval 2 ≤ t ≤ 8.
(b) Do the data in the table support the conclusion that train A’s velocity is -100 meters per minute at some time t with 5 < t < 8 ? Give a reason for your answer.
(c) At time t = 2, train A’s position is 300 meters east of the Origin Station, and the train is moving to the east.
Write an expression involving an integral that gives the position of train A, in meters from the Origin Station, at time t = 12. Use a trapezoidal sum with three subintervals indicated by the table to approximate the position of the train at time t = 12.
(d) A second train, train B, travels north from the Origin Station. At time t the velocity of train B is given by vB(t)= -5t2 + 60t + 25 , and at time t = 2 the train is 400 meters north of the station. Find the rate, in meters per minute, at which the distance between train A and train B is changing at time t = 2.
Answer/Explanation
Ans:
(a) Average accel = \(\frac{v_{A}(8)-v_{A}(2)}{8-2}=\frac{-120-100}{6}=-\frac{110}{3}m/min^{2}\)
(b) vA is differentiable ⇒ vA is continuous
vA (8) = -120 < – 100 < 40 = vA(5)
Therefore, by the Intermediate Value Theorem, there is a time t,
5 < t < 8, such that vA(t) = – 100.
(d) Let x be train A’s position, y train B’s position, and z the distance between train A and train B.
\(z^{2}= x^{2}+y^{2}\Rightarrow 2z\frac{dz}{dt}=2x\frac{dx}{dt}+2y\frac{dy}{dt}\)
x = 300, y = 400 ⇒ z = 500
vB (2) = -20 + 120 + 25 = 125
\(500\frac{dz}{dt}=(300)(100)+(400)(125)\)
\(500\frac{dz}{dt}=(300)(100)+(400)(125)\) meters per minute
Question
At time t ≥ 0, a particle moving along a curve in the xy-plane has position (x(t), y(t)) with velocity vector v(t) = (cos (t2), e0.5t). At t 1, the particle is at the point (3, 5).
(a) Find the x-coordinate of the position of the particle at time t = 2.
(b) For 0 < t < 1, there is a point on the curve at which the line tangent to the curve has a slope of 2. At what time is the object at that point?
(c) Find the time at which the speed of the particle is 3.
(d) Find the total distance traveled by the particle from time t = 0 to time t = 1.
Answer/Explanation
Ans:
(a) \(x(2)=3+\int_{1}^{2}cos(t^{2})dt=2.557 (or 2.556)\)
(b) \(\frac{dy}{dx}=\frac{dy/dt}{dx/dt}=\frac{e^{0.5t}}{cos(t^{2})}\)
\(\frac{e^{0.5t}}{cos(t^{2})}=2\)
t = 0.840
(c) \(Speed = \sqrt{cos^{2}(t^{2})+e^{t}}\)
\( \sqrt{cos^{2}(t^{2})+e^{t}}=3\)
t=2.196 (or 2.195)
(d) \( Distance = \int_{0}^{1}\sqrt{cos^{2}(t^{2})+e^{t}}dt = 1.595 (or 1.594)\)
Question
A particle moves such that its acceleration \(a(t)=1+\frac{1}{\sqrt{t}}\).The initial conditions are v(0)=2 and s(0)=10
(A) Find an expression for v(t).
(B) Find the position function s(t).
Answer/Explanation
(A)\(v(t)=\int (1+t^{-1/2})dt=\int dt+\int t^{-1/2}dt=t+\frac{t^{1/2}}{\frac{1}{2}}+C=t+2t^{1/2}+2\)
(B)\(s(t)=\int \left ( t+2t^{1/2}+2 \right )dt=\frac{1}{2}t^{2}+\frac{2t^{3/2}}{\frac{3}{2}}+2t+C=\frac{1}{2}t^{2}+\frac{4}{3}t^{3/2}+2t+10\)
Question
A particle begins accelerating from a point 100 units along the x-axis and an initial velocity of v(0) = 50. The acceleration is given by \(a(t)=15\sqrt{t}\).
(A) Find the velocity function of the particle.
(B) Find the position function of the particle.
(C) What is the change in velocity between time t = 0 and t = 5?
(D) What is the change in position from t = 0 to t = 5?
Answer/Explanation

Question
At time t, a particle moving in the xy-plane is at position ( x(t), y(t)), where x(t) and y(t) are not explicitly given. For t ≥ 0, \(\frac{dx}{dt}=4t + 1 and \frac{dy}{dt}= sin(t^{2}).\) At time t = 0, x(0) = 0 and y(0) = -4.
(a) Find the speed of the particle at time t = 3, and find the acceleration vector of the particle at time t = 3.
(b) Find the slope of the line tangent to the path of the particle at time t = 3.
(c) Find the position of the particle at time t = 3.
(d) Find the total distance traveled by the particle over the time interval 0 ≤ t ≤ 3.
Answer/Explanation
Ans:
(a)
\(Speed =\sqrt{(\frac{dy}{dt})^{2}+(\frac{dx}{dt})^{2}}\)
\(\frac{dy}{dt}|_{t=3}=sin(3^{2})=sin9\)
\(\frac{dx}{dt}|_{t=3}=4(3)+1=13\)
\(Speed|_{t=3}=\sqrt{(sin9)^{2}+(13)^{2}}\)
Speed = 13.007
Acceleration Vector = \(\left \langle \frac{d^{2}x}{dt^{2}},{\frac{d^{2}y}{dt^{2}}} \right \rangle\)
\(\frac{dx}{dt}=4t +1; \frac{d^{2}x}{dt^{2}}=4\)
\(\frac{dy}{dt}=sin(t^{2}); \frac{d^{2}y}{dt^{2}}=2t cos (t^{2})\)
\(\frac{d^{2}x}{dt^{2}}|_{t=3}=4; \frac{d^{2}y}{dt^{2}}|_{t=3}=-5.467\)
Acceleration vector = <4, -5.467>
(b)
From part A,
\(\frac{dx}{dt}=\frac{\left ( \frac{dy}{dt} \right )}{\left ( \frac{dx}{dt} \right )}\) \(\frac{dy}{dt}|_{t=3}=sin9\)
\(\frac{dx}{dt}|_{t=3}=13\)
\(\frac{dy}{dx}= \frac{sin9}{13}=0.0317\)
(c)
x position at t = 3 is equal to x(0) + \(\int_{0}^{3}\frac{dx}{dt}dt\)
y position at t = 3 is equal to y(0) + \(\int_{0}^{3}\frac{dy}{dt}dt\)
\(x(3)=0+\int_{0}^{3}(4t+1)dt=21\)
\(y(3)=-4+\int_{0}^{3}sin(t^{2})dt=-3.226\)
At t = 3, the particle’s position is (21, -3.226)
(d)
Distance Travelled = \(\int_{0}^{3}\sqrt{\left ( \frac{dx}{dt} \right )^{2}+\left ( \frac{dy}{dt} \right )^{2}}dt\)
\(=\int_{0}^{3}\sqrt{(4t+1)^{2}+sin^{2}(t^{2})}dt\)
Distance Travelled = 21.091
