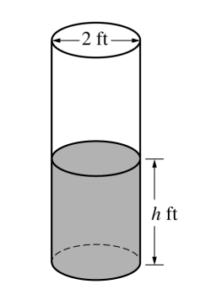
Question
A cylindrical barrel with a diameter of 2 feet contains collected rainwater, as shown in the figure above. The water drains out through a valve (not shown) at the bottom of the barrel. The rate of change of the height h of the water in the barrel with respect to time t is modeled by \(\frac{dh}{dt}=-\frac{1}{10}\sqrt{h},\) where h is measured in feet and
t is measured in seconds. (The volume V of a cylinder with radius r and height h is V = πr2h.)
(a) Find the rate of change of the volume of water in the barrel with respect to time when the height of the water is 4 feet. Indicate units of measure.
(b) When the height of the water is 3 feet, is the rate of change of the height of the water with respect to time increasing or decreasing? Explain your reasoning.
(c) At time t = 0 seconds, the height of the water is 5 feet. Use separation of variables to find an expression for h in terms of t.
Answer/Explanation
Ans:
(a) \(V = \pi r^{2}h=\pi (1)^{2}h=\pi h\)
\(\frac{dV}{dt}|_{h=4}=\pi \frac{dh}{dt}|_{h=4}=\pi \left ( -\frac{1}{10}\sqrt{4} \right )=-\frac{\pi }{5}\) cubic feet per second
(b) \(\frac{d^{2}h}{dt^{2}}=-\frac{1}{20\sqrt{h}}\cdot \frac{dh}{dt}=-\frac{1}{20\sqrt{h}}\cdot \left ( -\frac{1}{10} \sqrt{h}\right )=\frac{1}{200}\)
Because \(\frac{d^{2}h}{dt^{2}}=\frac{1}{200}>0\) for h > 0, the rate of change of the height is increasing when the height of the water is 3 feet.
(c) \(\frac{dh}{\sqrt{h}}=-\frac{1}{10}dt\)
\(\int \frac{dh}{\sqrt{h}}=\int -\frac{1}{10}dt\)
\(2\sqrt{h}=-\frac{1}{10}t+C\)
\(2\sqrt{5}=-\frac{1}{10}\cdot 0+C\Rightarrow C = 2\sqrt{5}\)
\(2\sqrt{h}=-\frac{1}{10}t+2\sqrt{5}\)
\(h(t)=\left ( -\frac{1}{20}t+\sqrt{5} \right )^{2}\)
Question
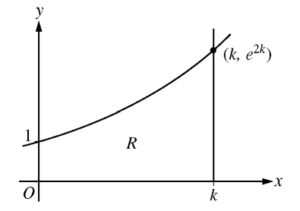
Let f(x) = e2x . Let R be the region in the first quadrant bounded by the graph of f, the coordinate axes, and the vertical line x = k, where k > 0. The region R is shown in the figure above.
(a) Write, but do not evaluate, an expression involving an integral that gives the perimeter of R in terms of k.
(b) The region R is rotated about the x-axis to form a solid. Find the volume, V, of the solid in terms of k.
(c) The volume V, found in part (b), changes as k changes. If \(\frac{dk}{dt}=\frac{1}{3}, determine \frac{dV}{t}when k=\frac{1}{2}.\)
Answer/Explanation
Ans:
(a)
\(\frac{dy}{dx}=2e^{2x}\)
\(p = 1 + k + e^{2x}+ \int_{0}^{k}\sqrt{1+(2e^{2x})^{2}}dx\)
(b)
u = 4x
\(\frac{du}{dx}=4\)
\(v = \int_{0}^{k}\pi r^{2}dx=\int_{0}^{k}\pi (e^{2x})^{2}dx=\pi \int_{0}^{k}e^{4x}dx\)
\(= \pi \int_{0}^{k}\frac{1}{4}e^{4}\cdot du=\frac{\pi }{4}\left [ e^{4x} \right ]_{0}^{k}=\frac{\pi }{4}\left ( e^{4k} -e^{4(0)}\right )\)
\(=\frac{\pi }{4}e^{4k}-1\left ( \frac{\pi }{4} \right )\)
\(v=\frac{\pi }{4}e^{4k}- \frac{\pi }{4}\)
(c)
\(\frac{dV}{dt}=\frac{dV}{dk}\cdot \frac{dk}{dt}=\frac{d}{dk}\left ( \frac{\pi }{4}e^{4k}-\frac{\pi }{4} \right )\cdot \left ( \frac{1}{3} \right )=\frac{\pi }{4}(4)e^{4k}\cdot \left ( \frac{1}{3} \right )\)
\(\frac{dV}{dt}=\frac{\pi }{3}e^{4k}|_{k=\frac{1}{2}}=\frac{\pi }{3}\cdot e^{2}\)
Question
Fish enter a lake at a rate modeled by the function E given by \(E(t)=20+15 sin(\frac{\pi t}{6}).\) Fish leave the lake at a rate modeled by the function L given by \(L(t)=4+2^{0.1t^{2}}.\) Both E(t) and L (t) are measured in fish per hour, and t is measured in hours since midnight (t = 0).
(a) How many fish enter the lake over the 5-hour period from midnight (t = 0) to 5 A.M. (t = 5) ? Give your answer to the nearest whole number.
(b) What is the average number of fish that leave the lake per hour over the 5-hour period from midnight (t = 0) to 5 A.M. (t = 5) ?
(c) At what time t, for 0 ≤ t ≤ 8, is the greatest number of fish in the lake? Justify your answer.
(d) Is the rate of change in the number of fish in the lake increasing or decreasing at 5 A.M. (t = 5) ? Explain your reasoning.
Answer/Explanation
Ans:
(a) \(\int_{0}^{5}E(t)dt=153.457690\)
To the nearest whole number, 153 fish enter the lake from midnight to 5 A.M.
(b) \(\frac{1}{5-0}\int_{0}^{5}L(t)dt=6.059038\)
The average number of fish that leave the lake per hour from midnight to 5 A.M. is 6.059 fish per hour.
(c) The rate of change in the number of fish in the lake at time t is given by E(t)-L(t) .
E(t)-L(t) =0⇒ t = 6.20356
E(t) – L(t) > 0 for 0 ≤ t < 6.20356, and E(t) – L(t) < 0 for 6.20356 < t ≤ 8. Therefore the greatest number of fish in the lake is at time 6.204 (or 6.203).
— OR —
Let A (t) be the change in the number of fish in the lake from midnight to t hours after midnight.
\(A(t)=\int_{0}^{t}(E(s)-L(s))ds\)
A'(t) = E(t) – L(t) = 0 ⇒ t = C = 6.20356
| t | A(t) |
0 C 8 | 0 135.01492 80.91998 |
Therefore the greatest number of fish in the lake is at time t = 6.204 (or 6.203).
(d) E'(5) – L'(5) = -10.7228 < 0
Because E ‘ (5) – L’ (5) < 0, the rate of change in the number of fish is decreasing at time t = 5.
Question
The rate at which rainwater flows into a drainpipe is modeled by the function R, where \(R(t)=20 sin \left ( \frac{t^{2}}{35} \right )\) cubic feet per hour, t is measured in hours, and 0 ≤ t ≤ 8. out the other end of the pipe at a rate modeled by D(t) = -0.04t3 + 0.4t2 + 0.96t cubic feet per hour, for 0 ≤ t ≤ 8. There are 30 cubic feet of water in the pipe at time t = 0.
(a) How many cubic feet of rainwater flow into the pipe during the 8-hour time interval 0 ≤ t ≤ 8 ?
(b) Is the amount of water in the pipe increasing or decreasing at time t = 3 hours? Give a reason for your answer.
(c) At what time t, 0 ≤ t ≤ 8, is the amount of water in the pipe at a minimum? Justify your answer.
(d) The pipe can hold 50 cubic feet of water before overflowing. For t > 8, water continues to flow into and out of the pipe at the given rates until the pipe begins to overflow. Write, but do not solve, an equation involving one or more integrals that gives the time w when the pipe will begin to overflow.
Answer/Explanation
Ans:
(a) \(\int_{0}^{8}R(t)dt=76.570\)
(b) R(3) – D(3) = -0.313632 < 0
Since R(3) < D(3), the amount of water in the pipe is decreasing at time t = 3 hours.
(c) The amount of water in the pipe at time t, 0 ≤ t ≤ 8, is
\(30+\int_{0}^{t}\left [ R(x)-D(x) \right ]dx.\)
R(t) – D(t) = 0 ⇒ t = 0, 3.271658
| t | Amount of water in the pipe |
0 3.271658 8 | 30 27.964561 48.543686 |
The amount of water in the pipe is a minimum at time t = 3.272 (or 3.271) hours.
(d) \(30+\int_{0}^{w}\left [ R(t)-D(t) \right ]dt.=50\)
Question
On a certain workday, the rate, in tons per hour, at which unprocessed gravel arrives at a gravel processing plant is modeled by \(G(t)=90+45 cos\left ( \frac{t^{2}}{18} \right ),\) where t is measured in hours and 0 ≤ t ≤ 8. At the beginning of the workday (t = 0) , the plant has 500 tons of unprocessed gravel. During the hours of operation, 0 ≤ t ≤ 8, the plant processes gravel at a constant rate of 100 tons per hour.
(a) Find G'(5) . Using correct units, interpret your answer in the context of the problem.
(b) Find the total amount of unprocessed gravel that arrives at the plant during the hours of operation on this workday.
(c) Is the amount of unprocessed gravel at the plant increasing or decreasing at time t = 5 hours? Show the work that leads to your answer.
(d) What is the maximum amount of unprocessed gravel at the plant during the hours of operation on this workday? Justify your answer.
Answer/Explanation
Ans:
(a) G'(5) = -24.588 (or – 24.587)
The rate at which gravel is arriving is decreasing by 24.588 (or 24.587) tons per hour per hour at time t=5 hours.
(b) \(\int_{0}^{8}G(t)dt=825.551 tons\)
(c) G(5) = 98.140764 < 100
At time t = 5, the rate at which unprocessed gravel is arriving is less than the rate at which it is being processed. Therefore, the amount of unprocessed gravel at the plant is
decreasing at time t = 5.
(d) The amount of unprocessed gravel at time t is given by
\(A(t)=500+\int_{0}^{t}(G(s)-100)ds.\)
A'(t) = G(t) – 100 = 0 ⇒ t = 4.923480

The maximum amount of unprocessed gravel at the plant during this workday is 635.376 tons.
Question
A T-shirt maker estimates that the weekly cost of making x shirts is \(C(x)=50+2x+\frac{x^{2}}{20}\). The weekly revenue from selling x shirts is given by the function: \(R(x)=20+\frac{x^{2}}{200}\). (Show your work.)
(A) Derive the weekly profit function.
(B) What is the maximum weekly profit?
Answer/Explanation
(A)\(P(x)=R(x)-C(x)\)
\(R(x)=20x+\frac{x^{2}}{200}\)
\(C(x)=50+2x+\frac{x^{2}}{20}\)
\(P(x)=20x+\frac{x^{2}}{200}-\left ( 50+2x+\frac{x^{2}}{20} \right )\)
\(P(x)=20x+\frac{x^{2}}{200}-50-2x-\frac{x^{2}}{20}\)
\(P(x)=18x-50-\frac{9x^{2}}{200}\)
(B)\(P(x)=18x-50-\frac{9x^{2}}{200}\)
\(P'(x)=18-(2)\left ( \frac{9x}{200} \right )\)
\(P'(x)=18-0.09x\)
\(0=18-0.09x\)
\(0.09x=18\)
x=200 shirts
\(P(200)=18(200)-50-\frac{9(200)^{2}}{200}\)
\(P(200)=3,600-50-1,800\)
\(P(200)=$1,750\)
Question
There is no snow on Janet’s driveway when snow begins to fall at midnight. From midnight to 9 A. M., snow accumulates on the driveway at a rate modeled by $f(t ) = 7te^{cost}$ cubic feet per hour, where t is measured in hours since midnight. Janet starts removing snow at 6 A. M. ( t =6) . The rate g( t), in cubic feet per hour, at which Janet removes snow from the driveway at time t hours after midnight is modeled by
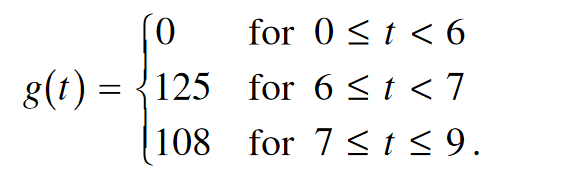
(a) How many cubic feet of snow have accumulated on the driveway by 6 A. M.?
(b) Find the rate of change of the volume of snow on the driveway at 8 A. M.
(c) Let h(t ) represent the total amount of snow, in cubic feet, that Janet has removed from the driveway at time t hours after midnight. Express h as a piecewise-defined function with domain \(0\leq t\leq 9\)
(d) How many cubic feet of snow are on the driveway at 9 A. M.?
Answer/Explanation
Ans:
(a) $\int_0^6 f(t) d t=142.274$ or $142.275$ cubic feet
(b) Rate of change is $f(8)-g(8)=-59.582$ or $-59.583$ cubic feet per hour.
(c) $h(0)=0$
For $0<t \leq 6, h(t)=h(0)+\int_0^t g(s) d s=0+\int_0^t 0 d s=0$
For $6<t \leq 7, h(t)=h(6)+\int_6^t g(s) d s=0+\int_6^t 125 d s=125(t-6)$.
For $7<t \leq 9, \quad h(t)=h(7)+\int_7^t g(s) d s=125+\int_7^t 108 d s=125+108(t-7)$
Thus, $h(t)= \begin{cases}0 & \text { for } 0 \leq t \leq 6 \\ 125(t-6) & \text { for } 6<t \leq 7 \\ 125+108(t-7) & \text { for } 7<t \leq 9\end{cases}$
(d) Amount of snow is $\int_0^9 f(t) d t-h(9)=26.334$ or $26.335$ cubic feet.