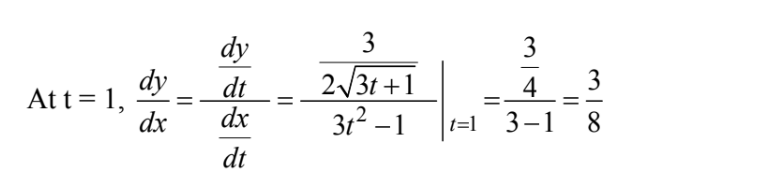Question
The asymptotes of the graph of the parametric equations \(x=\frac{1}{t},y=\frac{t}{t+1} \) are
(A) x=0, y = 0 (B) x = 0 only (C) x=-1 ,y=0 (D) x = −1 only (E)x= 0,y=1
Answer/Explanation
Ans:C
Question
If \(x=t^{2}-1 and y=2e^{t}, then\frac{dy}{dx}\)=
(A)\(\frac{e^{t}}{2}\) (B)\(\frac{2e^{t}}{t}\) (C)\(\frac{e^{|t|}}{t^{2}}\) (D) \(\frac{4e^{t}}{2t-1}\) (E)\(e^{t}\)
Answer/Explanation
Ans:A
Question
A particle moves in the xy-plane so that at any time t its coordinates are \(x= t^2-1\) and \(y=t^4-2t^3\) . At t =1, its acceleration vector is
(A) (0 , -1 ) (B) (0 , 12 ) (C) (2, −2 ) (D) (2,0) (E) (2,8)
Answer/Explanation
Ans:D
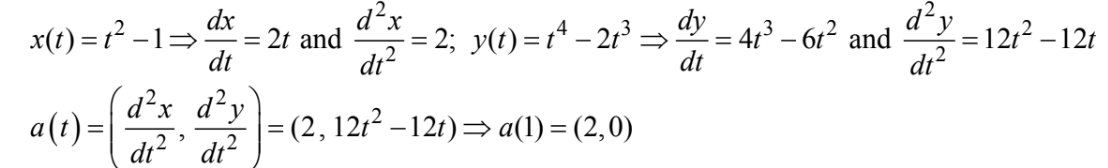
Question
If\( x=t^{3}-t \)and \(y=\sqrt{3t+1}\),then \(\frac{dy}{dt}\) at t=1 is
(A) \(\frac{1}{8}\) (B) \(\frac{3}{8}\) (C) \(\frac{3}{4}\) (D) \(\frac{8}{3}\) (E) 8
Answer/Explanation
Ans:B