Question
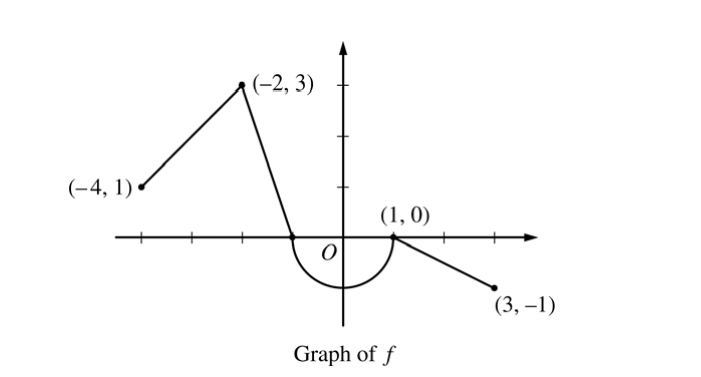
Let f be the continuous function defined on [-4, 3] whose graph, consisting of three line segments and a semicircle centered at the origin, is given above. Let g be the function given by \(g(x)=\int_{1}^{x}f(t)dt.\)
(a) Find the values of g(2) and g(-2).
(b) For each of g'(-3) and g”(-3) , find the value or state that it does not exist.
(c) Find the x-coordinate of each point at which the graph of g has a horizontal tangent line. For each of these points, determine whether g has a relative minimum, relative maximum, or neither a minimum nor a maximum at the point. Justify your answers.
(d) For -4 < x < 3, find all values of x for which the graph of g has a point of inflection. Explain your reasoning.
Answer/Explanation
Ans:
(a) \(g(2)=\int_{1}^{2}f(t)dt=-\frac{1}{2}(1)\left ( \frac{1}{2} \right )=-\frac{1}{4}\)
\(g(-2)=\int_{1}^{-2}f(t)dt=-\int_{-2}^{1}f(t)dt\)
\(= -\left ( \frac{3}{2}-\frac{\pi }{2} \right )=\frac{\pi }{2}-\frac{3}{2}\)
(b) \(g'(x)=f(x)\Rightarrow g'(-3)=f(-3)=2\)
\(g”(x)=f'(x)\Rightarrow g”(-3)=f'(-3)=1\)
(c) The graph of g has a horizontal tangent line where gx f'(x) = f(x) = 0. This occurs at x = −1 and x = 1.
g′(x ) changes sign from positive to negative at x = −1. Therefore, g has a relative maximum at x = −1.
g′(x) does not change sign at x = 1. Therefore, g has neither a relative maximum nor a relative minimum at x = 1.
(d) The graph of g has a point of inflection at each of x = −2, x = 0, and x = 1 because g′′(x) = f'(x) changes sign at each of these values.
