Question
The perimeter of an isosceles triangle is 16 cm. Do the following:
(A) Make a drawing of the problem.
(B) What are the dimensions of the sides and height for the maximum area?
(C) What is the maximum area?
Answer/Explanation
(A)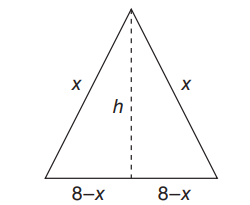
Given:P=16cm
P=2x+base
16=2x+base
base=16-2x
\(\frac{base}{2}=8-x\)
(B)\(x^{2}=h^{2}+(8-x)^{2}\)
\(x^{2}=h^{2}+(64-16x+x^{2})\)
\(x^{2}=h^{2}+64-16x+x^{2}\)
\(0=h^{2}+64-16x\)
\(h^{2}=16x-64\)
\(h^{2}=16(x-4)\)
\(h=4\sqrt{(x-4)}\)
\(A=\frac{1}{2}bh\)
\(A=\frac{1}{2}(16-2x)(4\sqrt{x-4})\)
\(A=(8-x)[2(x-4)^{\frac{1}{2}}]\)
\(\frac{\mathrm{d} A}{\mathrm{d} x}=\frac{1}{2}(2)(x-4)\frac{1}{2}(8-x)+(2)(x-4)^{\frac{1}{2}}(-1)\)
\(\frac{\mathrm{d} A}{\mathrm{d} x}=(x-4)^{\frac{1}{2}}(8-x)-(2)(x-4)^{\frac{1}{2}}\)
\(\frac{\mathrm{d} A}{\mathrm{d} x}=\frac{(8-x)-(2)(x-4)}{\sqrt{x-4}}\)
\(\frac{\mathrm{d} A}{\mathrm{d} x}=\frac{8-x-2x+8}{\sqrt{x-4}}\)
\(\frac{\mathrm{d} A}{\mathrm{d} x}=\frac{16-3x}{\sqrt{x-4}}\)
\(0=\frac{16-3x}{\sqrt{x-4}}\)
x=4 leads toan undefined solution
0=16-3x
3x=16
\(x=\frac{16}{3}=5.33cm\)
\(base=(16-2x)=\left [ 16-(2)\left ( \frac{16}{3} \right ) \right ]=\left [ 16-\frac{32}{3} \right ]=\left [ \frac{48}{3}-\frac{32}{3} \right ]=\frac{16}{3}=5.33cm\)
Therefor,the triangle is an equilateral triangle.
\(h=4\sqrt{(x-4)}=4\sqrt{\left ( \frac{16}{3}-4 \right )}=4\sqrt{\left ( \frac{16}{3} -\frac{12}{3}\right )}=4\sqrt{\frac{4}{3}}=\frac{8\sqrt{3}}{3}=4.62 cm\)
(C)\(A= \frac{1}{2}bh\)
\(A=\frac{1}{2}\left ( \frac{16}{3} \right )\left ( 4\sqrt{\frac{4}{3}} \right )\)
\(A=\left [ (2)\left ( \frac{16}{3} \right ) \sqrt{\frac{4}{3}}\right ]\)
\(A=\left [ \frac{32}{3}\sqrt{\frac{4}{3}} \right ]\)
A=(10.67cm)(1.16cm)
\(A=12.3cm^{2}\)
Question
The inside of a funnel of height 10 inches has circular cross sections, as shown in the figure above. At height h, the radius of the funnel is given by \(r = \frac{1}{20}(3+h^{2}),\) where 0 ≤ h ≤ 10. The units of r and h are inches.
(a) Find the average value of the radius of the funnel.
(b) Find the volume of the funnel.
(c) The funnel contains liquid that is draining from the bottom. At the instant when the height of the liquid is h =3 inches, the radius of the surface of the liquid is decreasing at a rate of \(\frac{1}{5}\) inch per second. At this instant, what is the rate of change of the height of the liquid with respect to time?
Answer/Explanation
Ans:
(a) Average radius \(= \frac{1}{10}\int_{0}^{10}\frac{1}{20}(3+h^{2})dh=\frac{1}{200}\left [ 3h+\frac{h^{3}}{3} \right ]_{0}^{10}\)
\(= \frac{1}{200}\left ( \left ( 30+\frac{1000}{3} \right )-0 \right )=\frac{109}{60}in\)
(b) \(Volume = \pi \int_{0}^{10}\left ( (\frac{1}{20})(3+h^{2}) \right )^{2}dh=\frac{\pi }{400}\int_{0}^{10}(9+6h^{2}+h^{4})dh\)
\(=\frac{\pi }{400}\left [ 9h + 2h^{3}+\frac{h^{5}}{5} \right ]_{0}^{10}\)
\(=\frac{\pi }{400}\left ( \left ( 90+2000+\frac{100000}{5} \right )-0 \right )=\frac{2209\pi }{40}in^{3}\)
(c) \(\frac{dr}{dt}=\frac{1}{20}(2h)\frac{dh}{dt}\)
\(-\frac{1}{5}=\frac{3}{10}\frac{dh}{dt}\)
\(\frac{dh}{dt}=-\frac{1}{5}\cdot \frac{10}{3}=-\frac{2}{3}in/sec\)
