Question
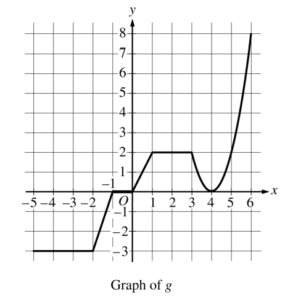
The graph of the continuous function g, the derivative of the function f, is shown above. The function g is piecewise linear for −5 ≤ x < 3, and g (x) = 2(x −4 ) 2 for 3 ≤ x ≤ 6.
(a) If f (1) = 3, what is the value of f(−5) ?
(b) Evaluate \(\int_{1}^{6}g(x)dx.\)
(c) For −5 < x < 6, on what open intervals, if any, is the graph of f both increasing and concave up? Give a reason for your answer.
(d) Find the x-coordinate of each point of inflection of the graph of f. Give a reason for your answer.
Answer/Explanation
Ans:
(a) \(f(-5)=f(1)+\int_{1}^{-5}g(x)dx=f(1)-\int_{-5}^{1}g(x)dx\)
\(=3-\left ( -9-\frac{3}{2}+1 \right )=3-\left ( -\frac{19}{2} \right )=\frac{25}{2}\)
(b) \(\int_{1}^{6}g(x)dx=\int_{1}^{3}g(x)dx+\int_{3}^{6}g(x)dx\)
\(=\int_{1}^{3}2dx+\int_{3}^{6}2(x-4)^{2}dx\)
\(=4+_{x=3}\left [ \frac{2}{3}(x-4)^{3} \right ]^{x=6}=4+\frac{16}{3}-\left ( -\frac{2}{3} \right )=10\)
(c) The graph of f is increasing and concave up on 0 < x < 1 and 4 < x < 6 because f ‘(x) =g(x)> 0 and f ‘(x) = g(x) is increasing on those intervals.
(d) The graph of f has a point of inflection at x = 4 because f'(x) = g(x) changes from decreasing to increasing at x = 4.
Question
There is no snow on Janet’s driveway when snow begins to fall at midnight. From midnight to 9 A. M., snow accumulates on the driveway at a rate modeled by $f(t ) = 7te^{cost}$ cubic feet per hour, where t is measured in hours since midnight. Janet starts removing snow at 6 A. M. ( t =6) . The rate g( t), in cubic feet per hour, at which Janet removes snow from the driveway at time t hours after midnight is modeled by
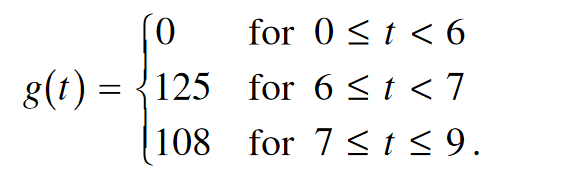
(a) How many cubic feet of snow have accumulated on the driveway by 6 A. M.?
(b) Find the rate of change of the volume of snow on the driveway at 8 A. M.
(c) Let h(t ) represent the total amount of snow, in cubic feet, that Janet has removed from the driveway at time t hours after midnight. Express h as a piecewise-defined function with domain \(0\leq t\leq 9\)
(d) How many cubic feet of snow are on the driveway at 9 A. M.?
Answer/Explanation
Ans:
(a) $\int_0^6 f(t) d t=142.274$ or $142.275$ cubic feet
(b) Rate of change is $f(8)-g(8)=-59.582$ or $-59.583$ cubic feet per hour.
(c) $h(0)=0$
For $0<t \leq 6, h(t)=h(0)+\int_0^t g(s) d s=0+\int_0^t 0 d s=0$
For $6<t \leq 7, h(t)=h(6)+\int_6^t g(s) d s=0+\int_6^t 125 d s=125(t-6)$.
For $7<t \leq 9, \quad h(t)=h(7)+\int_7^t g(s) d s=125+\int_7^t 108 d s=125+108(t-7)$
Thus, $h(t)= \begin{cases}0 & \text { for } 0 \leq t \leq 6 \\ 125(t-6) & \text { for } 6<t \leq 7 \\ 125+108(t-7) & \text { for } 7<t \leq 9\end{cases}$
(d) Amount of snow is $\int_0^9 f(t) d t-h(9)=26.334$ or $26.335$ cubic feet.
