Question
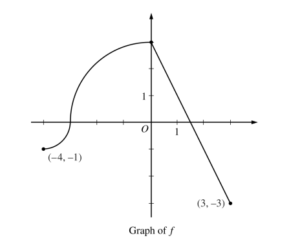
The continuous function f is defined on the closed interval −6 ≤ x ≤ 5. The figure above shows a portion of the graph of f, consisting of two line segments and a quarter of a circle centered at the point (5, 3). It is known that the point \(\left ( 3,3-\sqrt{5} \right )\) is on the graph of f.
(a) If \(\int_{-6}^{5}f(x)dx=7,\) find the value of \(\int_{-6}^{-2}f(x)dx\) Show the work that leads to your answer.
(b) Evaluate \(\int_{3}^{5}(2f'(x)+4)dx.\)
(c) The function g is given by \(\int_{-2}^{x}f(t)dt.\) Find the absolute maximum value of g on the interval − ≤ x ≤ 52 . Justify your answer.
(d) Find \(\lim_{x\rightarrow 1}\frac{10^{x}-3f'(x)}{f(x)-arctan x}.\)
Answer/Explanation
Ans:
(a) \(\int_{-6}^{5}f(x)dx=\int_{-6}^{-2}f(x)dx+\int_{-2}^{5}f(x)dx\)
\(\Rightarrow 7=\int_{-6}^{-2}f(x)dx+2+\left ( 9-\frac{9\pi }{4} \right )\)
\(\Rightarrow \int_{-6}^{-2}f(x)dx=7-\left ( 11-\frac{9\pi }{4} \right )=\frac{9\pi }{4}-4\)
(b) \(\int_{3}^{5}(2f'(x)+4)dx=2\int_{3}^{5}f'(x)+\int_{3}^{5}4dx\)
= 2 (f(5)- f(3)) + 4 (5-3)
\(=2(0-(3-\sqrt{5}))+8\)
\(=2(-3+\sqrt{5})+8=2+2\sqrt{5}\)
-OR-
\(\int_{3}^{5}(2f'(x)+4)dx=_{x=3}[2f(x)+4x]^{x=5}\)
=(2f(5) + 20) – (2 f(3) + 12)
\(=(2.0+20)-(2(3-\sqrt{5})+12)\)
\(=2+2\sqrt{5}\)
(c) \(g'(x)=f(x)=0\Rightarrow x=-1, x=\frac{1}{2}, x=5\)
| x | g(x) |
-2 -1 \(\frac{1}{2}\) 5 | 0 \(\frac{1}{2}\) \(-\frac{1}{4}\) \(11-\frac{9\pi }{4}\) |
On the interval -2 ≤ x ≤ 5, the absolute maximum value of g is g(5) = \(11-\frac{9\pi }{4}.\)
(d) \(\lim_{x\rightarrow 1}\frac{10^{x}-3f'(x)}{f(x)-arctan x}=\frac{10^{1}-3f'(1)}{f(1)-arctan 1}\)
\(=\frac{10-3.2}{1-arctan 1}=\frac{4}{1-\frac{\pi }{4}}\)
Question
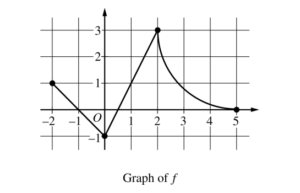
The function f is differentiable on the closed interval [−6, 5 ] and satisfies f (−2 )2 = 7. The graph of f ‘, the derivative of f, consists of a semicircle and three line segments, as shown in the figure above.
(a) Find the values of f (−6) and f (5).
(b) On what intervals is f increasing? Justify your answer.
(c) Find the absolute minimum value of f on the closed interval [−6, 5 ]. Justify your answer.
(d) For each of f “(−5) and f “(3), find the value or explain why it does not exist.
Answer/Explanation
Ans:
(a) \(f(-6)=f(-2)+\int_{-2}^{-6}f'(x)dx=7-\int_{-6}^{-2}f'(x)dx=7-4=3\)
\(f(5)=f(-2)+\int_{-2}^{5}f'(x)dx=7-2\pi +3=10-2\pi \)
(b) f ′ ( x) > 0 on the intervals [− 6, -2) and (2, 5). Therefore, f is increasing on the intervals [− 6, -2] and [2, 5] .
(c) The absolute minimum will occur at a critical point where f ‘ (x) = 0 or at an endpoint.
f ′( x) = 0 ⇒x = – 2, x = 2
| x | f(x) |
-6 -2 2 5 | 3 7 7-2π 10-2π |
The absolute minimum value is f (2) = 7 − 2π
(d) \(f”(-5)=\frac{2-0}{-6-(-2)}=-\frac{1}{2}\)
\(\lim_{x\rightarrow 3^{-}}\frac{f'(x)-f'(3)}{x-3}=2 and \lim_{x\rightarrow 3^{+}}\frac{f'(x)-f'(3)}{x-3}=-1\)
f ′′(3) does not exist because
\(\lim_{x\rightarrow 3^{-}}\frac{f'(x)-f'(3)}{x-3}\neq \lim_{x\rightarrow 3^{+}}\frac{f'(x)-f'(3)}{x-3}.\)
Question
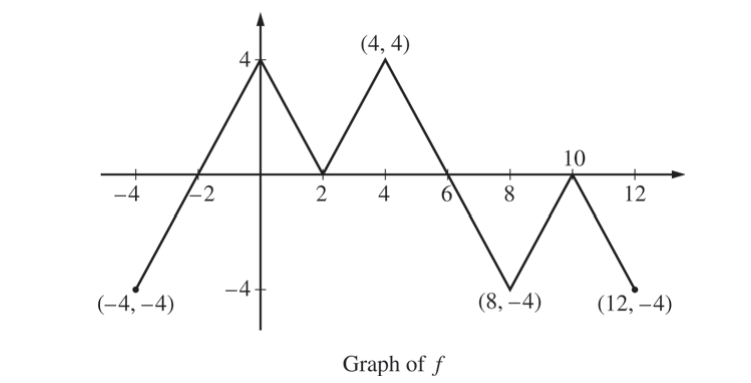
The figure above shows the graph of the piecewise-linear function f. For -4 ≤ x ≤ 12, the function g is defined by \(g(x)=\int_{2}^{x}f(t)dt.\)
(a) Does g have a relative minimum, a relative maximum, or neither at x = 10 ? Justify your answer.
(b) Does the graph of g have a point of inflection at x = 4 ? Justify your answer.
(c) Find the absolute minimum value and the absolute maximum value of g on the interval -4 ≤ x ≤ 12. Justify your answers.
(d) For -4 ≤ x ≤ 12, find all intervals for which g(x) ≤ 0.
Answer/Explanation
Ans:
(a) The function g has neither a relative minimum nor a relative maximum at x = 10 since g′ (x)= f(x) and f (x) ≤ 0 for 8 ≤ x ≤ 12.
(b) The graph of g has a point of inflection at x = 4 since g′(x) = f(x) is increasing for 2 ≤ x ≤ 4 and decreasing for 4 ≤ x ≤ 8.
(c) g′(x) = f(x) changes sign only at x = −2 and x = 6.
| x | g(x) |
-4 -2 6 12 | -4 -8 8 -4 |
On the interval −4 ≤ x ≤ 12, the absolute minimum value is g(−2) =− 8 and the absolute maximum value is g(6) = 8.
(d) g(x) ≤ 0 for −4 ≤ x ≤ 2 and 10 ≤ x ≤ 12.
Question
Consider the function \(f(x)=\frac{1}{x^{2}-kx},\) where k is a nonzero constant. The derivative of f is given by \(f'(x)=\frac{k-2x}{\left ( x^{2}-kx \right )^{2}}.\)
(a) Let k = 3, so that \(f(x)=\frac{1}{x^{2}-3x}.\) Write an equation for the line tangent to the graph of f at the point whose x-coordinate is 4.
(b) Let k = 4, so that \(f(x)=\frac{1}{x^{2}-4x}.\) Determine whether f has a relative minimum, a relative maximum, or neither at x = 2. Justify your answer.
(c) Find the value of k for which f has a critical point at x = -5.
(d) Let k = 6, so that \(f(x)=\frac{1}{x^{2}-6x}\) Find the partial fraction decomposition for the function f. Find \(\int f(x)dx.\)
Answer/Explanation
Ans:
(a) \(f(4)=\frac{1}{4^{2}-3\cdot 4}=\frac{1}{4}\) \(f'(4)=\frac{3-2\cdot 4}{\left ( 4^{2}-3\cdot 4 \right )^{2}}=-\frac{5}{16}\)
An equation for the line tangent to the graph of f at the point whose x-coordinate is 4 is \(y= -\frac{5}{16}(x-4)+\frac{1}{4}.\)
(b) \(f'(x)=\frac{4-2x}{\left ( x^{2}-4x \right )^{2}}\) \(f'(2)=\frac{4-2\cdot 2}{\left ( 2^{2}-4\cdot 2 \right )^{2}}=0\)
f'(x) changes sign from positive to negative at x = 2. Therefore, f has a relative maximum at x = 2.
(c) \(f'(-5)=\frac{k-2\cdot (5)}{\left ( (-5)^{2}-k\cdot (-5) \right )^{2}}=0\Rightarrow k = -10\)
(d) \(\frac{1}{x^{2}-6x}=\frac{1}{x(x-6)}=\frac{A}{x}+\frac{B}{x-6}\Rightarrow 1=A(x-6)+Bx\)
\(x = 0 \Rightarrow 1 = A\cdot (-6)\Rightarrow A = -\frac{1}{6}\)
\(x = 6 \Rightarrow 1 = B\cdot (6)\Rightarrow B = \frac{1}{6}\)
\(\frac{1}{x(c-6)}=\frac{-1/6}{x}+\frac{1/6}{x-6}\)
\(\int f(x)dx-\int \left ( \frac{-1/6}{x}+\frac{1/6}{x-6} \right )dx\)
\(=-\frac{1}{6}In|x| +\frac{1}{6}In|x-6|+C=\frac{1}{6}In\left | \frac{x-6}{x} \right |+C\)
Question
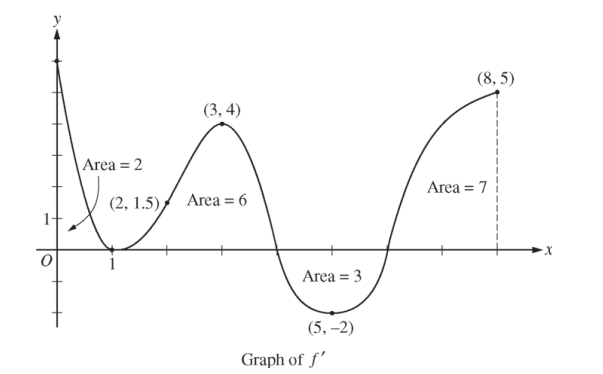
The figure above shows the graph of f’, the derivative of a twice-differentiable function f, on the closed interval 0 ≤ x ≤ 8. The graph of f’ has horizontal tangent lines at x = 1, x = 3, and x = 5. The areas of the regions between the graph of f’ and the x-axis are labeled in the figure. The function f is defined for all real numbers and satisfies f(8) = 4.
(a) Find all values of x on the open interval 0 < x < 8 for which the function f has a local minimum. Justify your answer.
(b) Determine the absolute minimum value of f on the closed interval 0 ≤ x ≤ 8. Justify your answer.
(c) On what open intervals contained in 0 < x < 8 is the graph of f both concave down and increasing? Explain your reasoning.
(d) The function g is defined by \(g(x)=(f(x))^{3}. If f(3)=-\frac{5}{2},\) find the slope of the line tangent to the graph of g at x = 3.
Answer/Explanation
Ans:
(a) x = 6 is the only critical point at which f’ changes sign from negative to positive. Therefore, f has a local minimum at x = 6.
(b) From part (a), the absolute minimum occurs either at x = 6 or at an endpoint.
\(f(0)=f(8)+\int_{8}^{0}f'(x)dx\)
\(f(8)-\int_{8}^{0}f'(x)dx=4-12 = -8\)
\(f(6)=f(8)+\int_{8}^{6}f'(x)dx\)
\(=f(8)-\int_{8}^{6}f'(x)dx=4-7=-3\)
f(8) = 4
The absolute minimum value of f on the closed interval [0, 8] is -8.
(c) The graph of f is concave down and increasing on 0< x < 1 and 3 < x < 4, because f’ is decreasing and positive on these intervals.
(d) \(g'(x)=3[f(x)]^{2}\cdot f'(x)\)
\(g'(3)=3[f(x)]^{2}\cdot f'(3)=3\left ( -\frac{5}{2} \right )^{2}\cdot 4=75\)
Question
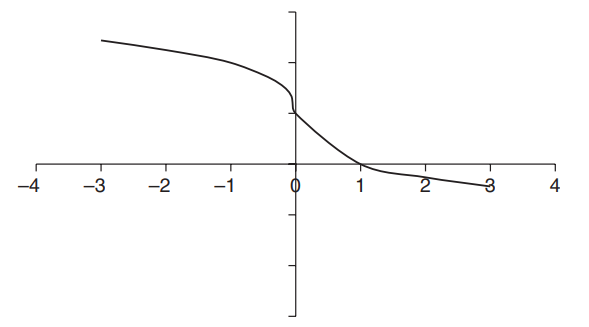
\(f(x)=1-\sqrt[3]{x}\)
(A) Find the intervals on which f is increasing or decreasing.
(B) Locate all maxima and minima.
(C) Find the intervals over which f is concave upward or downward.
(D) Find all inflection points.
(E) Sketch the graph of f.
Answer/Explanation
(A)Use the first derivative to find where f is increasing or decreasing. The first derivative \(f'(x)=\frac{1}{3}x^{-\frac{2}{3}}< 0\) for (-∞, +∞), then f is decreasing for all values of x.
(B) First, find any points where f ′(x) = 0, but f ′ < 0 for all values of x. At x = 0, f ′(x) does not exist since there is a zero in the denominator. Therefore, there are no maxima or minima.
(C) Use the second derivative to test for concavity.\)f”(x)=\frac{2}{9}x^{-\frac{5}{3}}\).f”>0 when x > 0; therefore, f is concave upward on the interval (0, +∞). If x < 0, then f ″ < 0; therefore, f is concave downward on (-∞, 0).
(D) The second derivative f ″ changes concavity at x = 0, so there is an inflection point at x = 0. The function f (0) = 1, so the inflection point is at coordinate (0, 1), which is also the y-intercept.
(E) y-intercept at (0, 1). x-intercept at (1, 0).
Question
Given the graph of f ′, find the following properties of the function f :
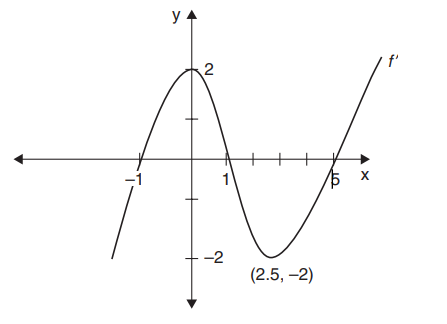
(A) The intervals on which f is increasing or decreasing
(B) The location of the relative maxima and minima
(C) The points of inflection and concavity of f
(D) Draw a sketch of f , given that f (-1) = f (1) = 5, f (0) = 0, and f (5) = -5.
Answer/Explanation
(A) f ′ < 0 on (-∞, -1) and (1, 5), so f is decreasing. f ′ > 0 on (-1, 1) and (5, +∞), so f is increasing.
(B) The function has a relative maximum at x = 1 since f ′ changes from positive to negative. There are relative minima at x = (-1, 5) since f ′ changes from negative to positive.
(C) f ′ is increasing on (-∞, 0), so f ′′ > 0 and f is concave upward. f ′ is decreasing on \(\left ( 0,2\frac{1}{2} \right )\) so f ′′ < 0 and f is concave downward. f ′ is increasing on\(\left ( 2\frac{1}{2} ,+\infty \right ) \), so f ′′ > 0 and f is concave upward. A change of concavity occurs at x = 0 and \(x=2\frac{1}{2}\) .Summarizing the results in a table:
Question
\(f(x) =x^{4}-x^{3}\).
(A) Find the intervals on which f is increasing or decreasing.
(B) Locate all maxima and minima.
(C) Find the points of inflection, if any, on f .
(D) Find the intervals where f is concave upward or downward.
(E) Sketch the graph of \(f(x) =x^{4}-x^{3}\).
Answer/Explanation
(A) To figure out where f (x) is increasing or decreasing, set \(f'(x)=4x^{3}-3x^{2}=x^{2}(4x-3)=0\)
The function equals zero at x = 0 and x = 3. Use a test point on each interval to find where f (x) is increasing or decreasing. The function f (x) is increasing on interval \(\left ( \frac{3}{4},\infty \right )\)
but is decreasing for interval (-∞, 0) and decreasing for \(\left ( 0,\frac{3}{4}\right )\).

B) You found in part (a) that f ′(x) = 0 at x = 0 and \(x=\frac{3}{4}\) . You then take the second derivative at those points to determine if they represent a maximum or minimum.You find that \(f{}”(x)=12x^{2}-6x\) You then substitute values for x to find that f ′′(0) = 0 and \(f”\left ( \frac{3}{4} \right )=\frac{9}{4}\). This demonstrates that \(f\left ( \frac{3}{4} \right )\) is a relative minimum. The test for f ′′(0) is inconclusive, so look back to the first derivative. The first derivative changes from positive to negative at x = 0, which implies that x = 0 is a relative maximum. At \(x=\frac{3}{4}\) ,f’=0 \(f”\left (\frac{3}{4}\right )=12\left ( \frac{9}{16} \right )-6\left ( \frac{3}{4} \right )=\frac{108}{16}-\frac{72}{16}=\frac{36}{16}> 0\) so \(\frac{3}{4}\) is a relative minimum.\(f\left ( \frac{3}{4} \right )=\left ( \frac{3}{4} \right )^{2}-\left ( \frac{3}{4} \right )^{4}-\left ( \frac{3}{4} \right )^{3}=\frac{81}{256}-\frac{108}{256}=-\frac{27}{256},\)so relative minimum at \(f\left ( \frac{3}{4} \right )=-\frac{27}{256}\).

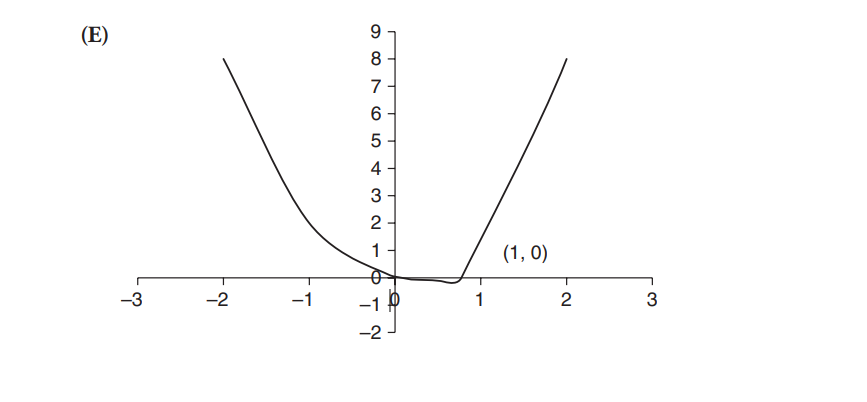
Question
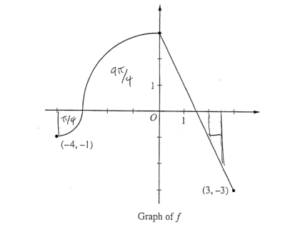
The continuous function f is defined on the interval \(-4\leq x\leq 3.\) The graph of f consists of two quarter circles and one line segment, as shown in the figure above. Let \(g(x)=2x+\int_{0}^{x}f(t)dt.\)
(a) Find g(-3). Find g’(x) and evaluate g’(-3).
(b) Determine the x-coordinate of the point at which g has an absolute maximum on the interval \(-4\leq x\leq 3.\)
(c) Find all values of x on the interval -4 < x < 3 for which the graph of g has a point of inflection. Give a reason for your answer. (d) Find the average rate of change of f on the interval \(-4\leq x\leq 3.\) There is no point c, -4 < c < 3, for which f’(c) is equal to that average rate of change. Explain why this statement does not contradict the Mean Value Theorem.
Answer/Explanation
Ans:
(a)
\(g(-3)=2\cdot (-3)+\int_{0}^{-3}f(t)dt=-6-\frac{9\pi }{4}\)
\(g'(x)=d/dx \left ( 2x+\int_{0}^{x}f(t)dt \right )=2+f(x)\)
g'(-3) = 2 + f(-3) = 2 + 0 = 2
(b)
g'(x) = 0 2 + f(x) = 0
f(x) = -2
x = 5/2
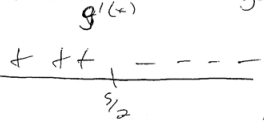
x = 5/2, because g’ check endpoints going from t to – proves it as the only relative maximum and g(5/2) is greater than g at either end point.
\(g(-4)= -8+\int_{0}^{-4}f(t)dt\)
= -8 – 2π
\(g(5/2)= 5+\int_{0}^{5/2}f(t)dt=5+\frac{5}{4}\)
\(g(3)= 6+\int_{0}^{3}f(t)dt=6\)
(c)
g”(x) = d/dx (g(x)) = f'(x)
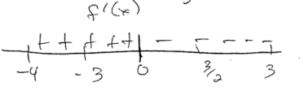
The only point of inflection for g is at x = 0, since f'(x), which is equivalent to g”, only changes signs at x = 0 on the interval -4 ≤ x ≤3
(d)
Avg. Rate of change = \(\frac{f(x)-f(-4)}{3-(-4)}\)
\(=\frac{-3–1}{3+4}=\frac{-2}{7}\)
Because Mean value Theorem only applies when the function is continuous AND differentiable on the interval, which doesn’t apply here since f(x) isn’t differentiable at x = 0.
Question
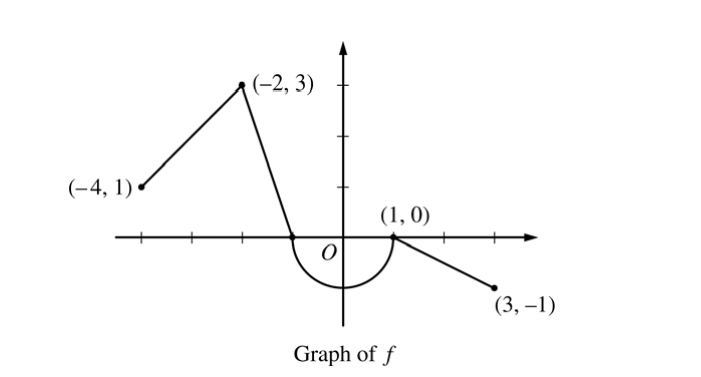
Let f be the continuous function defined on [-4, 3] whose graph, consisting of three line segments and a semicircle centered at the origin, is given above. Let g be the function given by \(g(x)=\int_{1}^{x}f(t)dt.\)
(a) Find the values of g(2) and g(-2).
(b) For each of g'(-3) and g”(-3) , find the value or state that it does not exist.
(c) Find the x-coordinate of each point at which the graph of g has a horizontal tangent line. For each of these points, determine whether g has a relative minimum, relative maximum, or neither a minimum nor a maximum at the point. Justify your answers.
(d) For -4 < x < 3, find all values of x for which the graph of g has a point of inflection. Explain your reasoning.
Answer/Explanation
Ans:
(a) \(g(2)=\int_{1}^{2}f(t)dt=-\frac{1}{2}(1)\left ( \frac{1}{2} \right )=-\frac{1}{4}\)
\(g(-2)=\int_{1}^{-2}f(t)dt=-\int_{-2}^{1}f(t)dt\)
\(= -\left ( \frac{3}{2}-\frac{\pi }{2} \right )=\frac{\pi }{2}-\frac{3}{2}\)
(b) \(g'(x)=f(x)\Rightarrow g'(-3)=f(-3)=2\)
\(g”(x)=f'(x)\Rightarrow g”(-3)=f'(-3)=1\)
(c) The graph of g has a horizontal tangent line where gx f'(x) = f(x) = 0. This occurs at x = −1 and x = 1.
g′(x ) changes sign from positive to negative at x = −1. Therefore, g has a relative maximum at x = −1.
g′(x) does not change sign at x = 1. Therefore, g has neither a relative maximum nor a relative minimum at x = 1.
(d) The graph of g has a point of inflection at each of x = −2, x = 0, and x = 1 because g′′(x) = f'(x) changes sign at each of these values.