Question
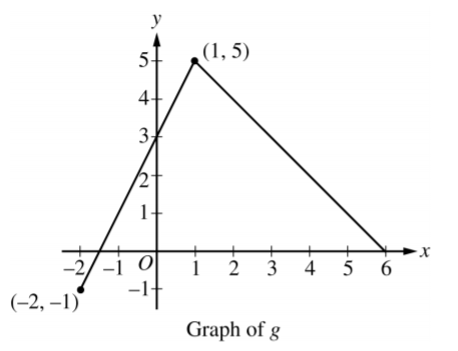
The graph of the function g is shown above. If f is the function given by f(x) =g(g(x)) , what is the value of f'(0) ?
A −2
B −1
C 2
D 3
Answer/Explanation
Question
If \(g(x)=2ln(x+1)\) and f is a differentiable function of x, which of the following is equivalent to the derivative of f(g(x)) with respect to x ?
A \({f}'(\frac{2}{x+1})\)
B \(\frac{2{f}'(x)}{x+1}\)
C \({f}'(2ln(x+1))\)
D \(\frac{2{f}'(2ln(x+1))}{x+1}\)
Answer/Explanation
Ans:D
Question
For which of the following functions is the chain rule an appropriate method to find the derivative with respect to x ?
I. \(y=cos(\sqrt{x}+1)\)
II. \(y=2^xsinx\)
III. \(y=\frac{20}{40x^2−1}\)
A. I only
B. II only
C. III only
D. I and III only
Answer/Explanation
Ans:D
Each of the functions in I and III is a composition of component functions. In I, let \(f(x)=cosx\)
Question
Let f be a differentiable function. If \(h(x)=(2+f(sinx))^3\), which of the following gives a correct process for finding \(h′(x)\) ?
A \(h′(x)=3(2+f(sinx))^2\)
B \(h′(x)=3(2+f(sinx))^2⋅f′(sinx)\)
C \(h′(x)=3(2+f(sinx))^2⋅f′(cosx)\)
D \(h′(x)=3(2+f(sinx))^2⋅f′(sinx)⋅cosx\)
Answer/Explanation
Ans:D
