Question
The marginal cost of producing x units of an item is \(C'(x)=\frac{1}{4}x-2\)
(A) Find an expression for C(x), assuming the cost of producing 0 units is $2, such that C(0) = 2.
(B) Find the value of x such that the average cost is a minimum. Justify your answer.
(C) Find the cost for producing 40 units.
Answer/Explanation
(A)\(C(x)=\int C'(x)dx=\int \left ( \frac{1}{4}x-2 \right )dx=\frac{1}{8}x^{2}-2x+C=\frac{1}{8}x^{2}-2x+2\)
(B)\(\bar{C}=\frac{C(x)}{x}=\frac{x}{8}-2+\frac{2}{x}.\) Set \(\frac{\mathrm{d} \bar{C}}{\mathrm{d} x}\)equal to zero to find the minimum average cost.\( \frac{\mathrm{d} \bar{C}}{\mathrm{d} x}=\frac{1}{8}-\frac{2}{x^{2}}=0\)Solving for x, one obtains x = 4. Find the second derivative at this point to confirm it’s a relative minimum:\(\frac{\mathrm{d} ^{2}\bar{C}}{\mathrm{d} x^{2}}=\frac{4}{x^{3}}\).At x = 4, this second derivative is positive; therefore, it is concave up and a relative minimum. The value of x such that the average cost is a minimum is 4.
(C)\(C(40)=\frac{40^{2}}{8}-2(40)+2=122\)
Question
A virus population is growing at a rate of \(P'(t)=10t-2\sqrt{t}+100\) organisms per hour every t hours.
(A) If the initial population, P(0), is 500, what is the population after t hours?
(B) What is the increase in population after 3 hours, rounded to the nearest whole number?
(C) What is the average rate of change in the population during first 12 hours?
Answer/Explanation
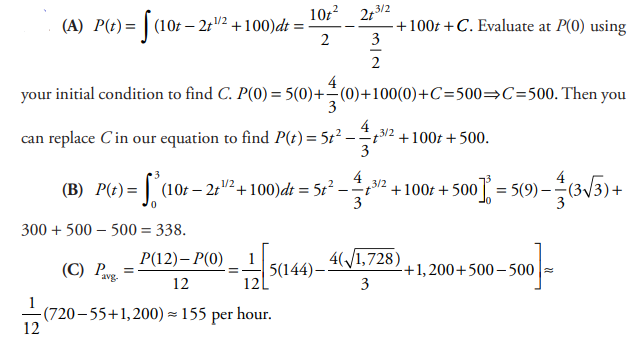
Question
A pillar is 35 ft tall. The density of the pillar is given by \(\rho (x)=\frac{1}{3\sqrt{x+1}}\) where x is the distance from the ground (x = 0) in feet and the mass is measured in tons. Assume that the volume is constant over the length of the pillar.
(A) What is the total mass of the pillar rounded to the nearest ton?
(B) For what value of height, h, does the interval [0, h] contain half the total mass of the pillar?
(C) What is the mass of the uppermost 5 ft of the pillar, rounded to the nearest hundredth?
Answer/Explanation
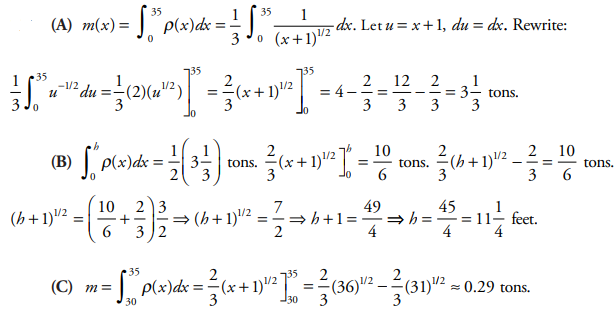
Question
The rate of change in temperature of a greenhouse from 7 p.m. to 7 a.m. is given by the function: \(f(t)=-3\sin \left ( \frac{t}{3} \right )\) where temperature is measured in degrees Fahrenheit and t is the number of hours after 7 p.m.
(A) If at 7 p.m. the temperature is 1058F, find the temperature of the greenhouse at 2 a.m.
(B) Write an integral expression to represent the temperature of the greenhouse at time t, where t is between 7 p.m. and 7 a.m.
(C) Find the average change in temperature of the greenhouse between 7 p.m. and 7 a.m. to the nearest 10th of a degree.
(D) Is there a point during the night when the rate of change it temperature of the greenhouse is the average change in temperature from part (c)? If yes, state the time. Either way, show all work to justify your answer.Ans:
Answer/Explanation
(A)F(0)=105,f(t) represents the rate of change of the temperature, and 2 a.m. is 7h after 7p.m.
\(F(7)=105+\int_{0}^{7}(-3\sin (t/3))dt\Rightarrow F(7)=105+9\cos (t/3)|^{7}_{0}\Rightarrow F(7)\approx 89.78\)
(B)\(F(t)=105+\int_{0}^{t}(-3\sin (x/3))dx\)
(C) Average value=\(\frac{1}{12-0}\int_{0}^{12}(-3\sin (t/3))dt\approx -1.24^{\circ}F/hour\)
(D) Since f(t) is continuous on [0, 12], by the Mean Value Theorem for integrals there
exists a number c in [0, 12] such that \(\int_{0}^{12}f(t)dt=f(c)(b-a)\)
You can use our solution from part (d) to show that f(c)=-1.24. Now solve for c.
\(f(c)=-1.24\Rightarrow -3\sin (t/3)=-1.24\Rightarrow \sin (t/3)=0.413\Rightarrow t/3=\sin ^{-1}(0.413)\Rightarrow t\approx 1.28\)
Approximately 1.28 h after 7 p.m., the rate of change of the temperature in the greenhouse equals the average rate of change of the temperature for the night. Now convert 0.28 to minutes to find the time.
\((0.28h)\times (60)=16.8min\approx 17 min\)
