Question
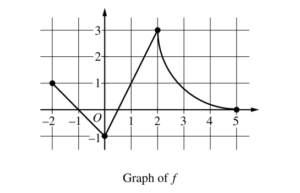
The continuous function f is defined on the closed interval −6 ≤ x ≤ 5. The figure above shows a portion of the graph of f, consisting of two line segments and a quarter of a circle centered at the point (5, 3). It is known that the point \(\left ( 3,3-\sqrt{5} \right )\) is on the graph of f.
(a) If \(\int_{-6}^{5}f(x)dx=7,\) find the value of \(\int_{-6}^{-2}f(x)dx\) Show the work that leads to your answer.
(b) Evaluate \(\int_{3}^{5}(2f'(x)+4)dx.\)
(c) The function g is given by \(\int_{-2}^{x}f(t)dt.\) Find the absolute maximum value of g on the interval − ≤ x ≤ 52 . Justify your answer.
(d) Find \(\lim_{x\rightarrow 1}\frac{10^{x}-3f'(x)}{f(x)-arctan x}.\)
▶️Answer/Explanation
Ans:
(a) \(\int_{-6}^{5}f(x)dx=\int_{-6}^{-2}f(x)dx+\int_{-2}^{5}f(x)dx\)
\(\Rightarrow 7=\int_{-6}^{-2}f(x)dx+2+\left ( 9-\frac{9\pi }{4} \right )\)
\(\Rightarrow \int_{-6}^{-2}f(x)dx=7-\left ( 11-\frac{9\pi }{4} \right )=\frac{9\pi }{4}-4\)
(b) \(\int_{3}^{5}(2f'(x)+4)dx=2\int_{3}^{5}f'(x)+\int_{3}^{5}4dx\)
= 2 (f(5)- f(3)) + 4 (5-3)
\(=2(0-(3-\sqrt{5}))+8\)
\(=2(-3+\sqrt{5})+8=2+2\sqrt{5}\)
-OR-
\(\int_{3}^{5}(2f'(x)+4)dx=_{x=3}[2f(x)+4x]^{x=5}\)
=(2f(5) + 20) – (2 f(3) + 12)
\(=(2.0+20)-(2(3-\sqrt{5})+12)\)
\(=2+2\sqrt{5}\)
(c) \(g'(x)=f(x)=0\Rightarrow x=-1, x=\frac{1}{2}, x=5\)
| x | g(x) |
-2 -1 \(\frac{1}{2}\) 5 | 0 \(\frac{1}{2}\) \(-\frac{1}{4}\) \(11-\frac{9\pi }{4}\) |
On the interval -2 ≤ x ≤ 5, the absolute maximum value of g is g(5) = \(11-\frac{9\pi }{4}.\)
(d) \(\lim_{x\rightarrow 1}\frac{10^{x}-3f'(x)}{f(x)-arctan x}=\frac{10^{1}-3f'(1)}{f(1)-arctan 1}\)
\(=\frac{10-3.2}{1-arctan 1}=\frac{4}{1-\frac{\pi }{4}}\)
